2023年浙教版数学八年级上册1.5 三角形全等的判定 同步测试（提高版）
试卷更新日期：2023-08-13 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 下列生活实例中，利用了“三角形稳定性”的是（ ）A、
B、
C、
D、
2. 如图，小亮进行以下操作：以点A为圆心，适当长为半径作圆弧分别交AB， AC于点D，E；分别以点D，E为圆心，大于DE长为半径作圆弧，两条圆弧交于∠BAC内一点F，作射线AF．若∠BDF=50°，∠EFD-∠BAC=24°，则∠BAC等于（ ）
A、26° B、31° C、37° D、38°3. 如图是某纸伞截面示意图，伞柄AP平分两条伞骨所成的角∠BAC．若支杆DF需要更换，则所换长度应与哪一段长度相等（ ）
A、BE B、AE C、DE D、DP4. 如图，点A、D、C、E在同一条直线上， ， ， 则的长为（ ）
A、 B、 C、 D、5. 如图所示，AB∥CD，AD∥BC，BE＝DF，则图中全等三角形共有（ ）对．
A、2 B、3 C、4 D、16. 有一张三角形纸片ABC，已知∠B＝∠C＝x°，BC＝5，按下列方案用剪刀沿着箭头的方向剪开该纸片，得不到全等三角形纸片的是（ ）A、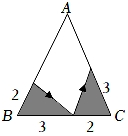
B、
C、
D、
7. 如图，在△ABC中，点D为BC的中点，△AEF的边EF过点C，且AE=EF，AB∥EF，AD平分∠BAE，CE=3，AB=13，则CF=（ ）
A、10 B、8 C、7 D、68. 如图，平分 ， 于点 ， 若 ， 点是边上一动点，关于线段叙述正确的是（ ）
A、 B、 C、 D、9. 如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD．若CD=AC，∠A=50°，则∠ACB的度数为（ ）
A、 B、 C、 D、10. 如图，把两根钢条 ， 的中点连在一起，可以做成一个测量工件内槽宽的卡钳，卡钳的工作原理是全等三角形的判定定理，其依据是（ ）
A、 B、 C、 D、二、填空题（每题4分，共24分）
-
11. 如图，在△ABC中，AB＝10，AC＝6，则BC边上的中线AD的取值范围是.
12. 如图，点D是等腰的边BC上的一点，过点B作于点E，连接CE，若 ， 则的值是 ．
13. 如图，在中，是边上的高，平分 ， 交于点E， ， 若的面积为9，则的长为.
14. 在中，的垂直平分线分别交 ， 于点、 ， 的垂直平分线分别交 ， 于点、 ， 若 ， ， 且的周长为16，求.
15. 沛沛沿一段笔直的人行道行走，边走边欣赏风景，在由C走到D的过程中，通过隔离带的空隙P ， 刚好浏览完对面人行道宣传墙上的一条标语，具体信息如下：如图，//// ， 相邻两平行线间的距离相等，AC ， BD相交于P ， 垂足为D.已知米.请根据上述信息求标语AB的长度.
16. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)．你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块。依据 。
三、解答题（共8题，共66分）
-
17. 根据要求回答下列问题：(1)、工程建筑中经常采用三角形的结构，如屋顶的钢架，输电线的支架等，这里运用的三角形的性质是 ；(2)、下列图形具有稳定性的有 个：
正方形、长方形、直角三角形、平行四边形
(3)、要使五边形木架（用5根木条钉成）不变形，工人准备再钉上两根木条，如图的两种钉法中正确的是： ；
(4)、要使四边形木架（用4根木条钉成）不变形，至少需要加1根木条固定，要使五边形木架不变形，至少需要加2根木条固定，要使六边形木架不变形，至少需要加3根木条固定，…，如果要使一个n边形木架不变形，至少需要加 根
18. 如图，点B，F，C，E在同一条直线上，点A，D在直线BC的异侧，AB＝DE，AC＝DF，BF＝EC.
(1)、求证：△ABC≌△DEF；(2)、若∠BFD＝130°，求∠ACB的度数.19. 如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得EF＝ED，连CF.
(1)、求证：CF∥AB(2)、若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数.20. 如图，在四边形中，P为边上的一点，.、分别是、的角平分线.
(1)、若 ， 则的度数为 ， 的度数为；(2)、求证：；(3)、设 ， ， 过点P作一条直线，分别与 ， 所在直线交于点E、F，若 ， 直接写出的长（用含a的代数式表示）21. 如图：
(1)、如图1，∠MAN＝90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；(2)、如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，且∠1＝∠2＝∠BAC．求证：△ABE≌△CAF；
(3)、如图3，在△ABC中，AB＝AC，AB＞BC．点D在边BC上，CD＝2BD，点E、F在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为21，求△ACF与△BDE的面积之和．22. 问题情境：如图1，在直角三角形ABC中，∠BAC＝90°，AD⊥BC于点D，可知：∠BAD＝∠C（不需要证明）；
(1)、特例探究：如图2，∠MAN＝90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D.证明：△ABD≌△CAF；(2)、归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB＝AC，∠1＝∠2＝∠BAC.求证：△ABE≌△CAF；(3)、拓展应用：如图4，在△ABC中，AB＝AC，AB＞BC.点D在边BC上，CD＝2BD，点E、F在线段AD上，∠1＝∠2＝∠BAC.若△ABC的面积为3，则△ACF与△BDE的面积之和为.23. 已知：在△ABC中，BD是边AC的高，BE为∠CBD的角平分线，且AD＝DE ． AO为△ABC的中线，延长AO到点F ． 使得BF∥AC ． 连接EF ． EF交BC于点G ． AF交BE于点H ．
(1)、求证：BF＝CD+DE；
(2)、求证：∠FBE＝∠BAC
(3)、若∠C＝45°．求证：BD＝BG ．
24. 以△ABC的AB，AC为边作△ABD和△ACE，且AD＝AB，AE＝AC，∠DAB＝∠CAE＝α.CD与BE相交于O，连接AO，如图①所示.
(1)、求证：BE＝CD；(2)、判断∠AOD与∠AOE的大小，并说明理由.(3)、在EB上取使F，使EF＝OC，如图②，请直接写出∠AFO与α的数量关系.