2023年浙教版数学八年级上册1.5 三角形全等的判定 同步测试(培优版)
试卷更新日期:2023-08-13 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
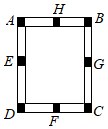 A、 两点之间 B、 两点之间 C、 两点之间 D、 两点之间2. 阅读以下作图步骤:
A、 两点之间 B、 两点之间 C、 两点之间 D、 两点之间2. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且3. 如图,中, , , 三条角平分线、、交于 , 于下列结论:;;平分;其中正确的结论个数有( )
A、且 B、且 C、且 D、且3. 如图,中, , , 三条角平分线、、交于 , 于下列结论:;;平分;其中正确的结论个数有( )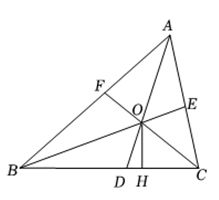 A、1个 B、2个 C、3个 D、4个4. 如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A、1个 B、2个 C、3个 D、4个4. 如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( ) A、7 B、 C、8 D、95. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( )
A、7 B、 C、8 D、95. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( ) A、 B、2 C、 D、36. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( )
A、 B、2 C、 D、36. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( ) A、5 B、5.5 C、6 D、77. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .
A、5 B、5.5 C、6 D、77. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .对于三人的答案,下列结论正确的是( )
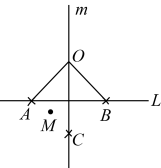 A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确8. 如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点 , 若 , 则等于( )
A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确8. 如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点 , 若 , 则等于( ) A、 B、 C、 D、9. 给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )A、 , B、 , C、 , D、 ,10. 乐乐所在的七年级某班学生到野外活动,为测量池塘两端 , 的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:
A、 B、 C、 D、9. 给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )A、 , B、 , C、 , D、 ,10. 乐乐所在的七年级某班学生到野外活动,为测量池塘两端 , 的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:乐乐:如图 , 先在平地取一个可直接到达 , 的点 , 再连接 , , 并分别延长至 , 至 , 使 , , 最后测出的长即为 , 的距离.
明明:如图 , 先过点作的垂线 , 再在上取 , 两点,使 , 接着过点作的垂线 , 交的延长线于点 , 则测出的长即为 , 的距离.
聪聪:如图 , 过点作 , 再由点观测,在的延长线上取一点 , 使这时只要测出的长即为 , 的距离.
以上三位同学所设计的方案中可行的是( )
 A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行
A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行二、填空题(每空4分,共24分)
-
11. 如图,已知D是△ABC的边BC上一点,且 , , AE是△ABD的中线,若 , 则 .
 12. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .
12. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .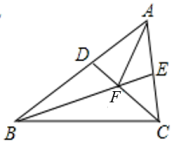 13. 如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E, , 则的度数为 . (用含的式子表示)
13. 如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E, , 则的度数为 . (用含的式子表示) 14. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
14. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度. 15. 在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E,则∠AEB=︒
15. 在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E,则∠AEB=︒ 16. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
16. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .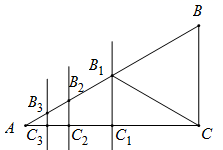
三、解答题(共8题,共66分)
-
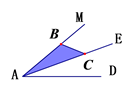
17.(1)、如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
 (2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
(2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.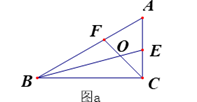 (3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
(3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.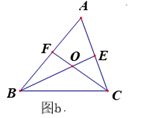 18. 要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?19. 已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
18. 要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?19. 已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明. 20. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
20. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .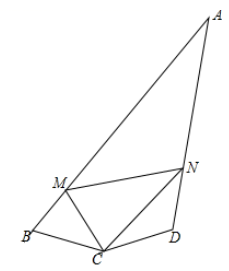 21. 如图(1), , , 垂足分别为、 , 点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束 .
21. 如图(1), , , 垂足分别为、 , 点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束 . (1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.22. 已知 , 点为平面内一点,于 .
(1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.22. 已知 , 点为平面内一点,于 . (1)、如图1,直接写出和之间的数量关系;(2)、如图2,过点作于点 , 求证:;(3)、如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分 , 平分 , 若 , , 直接写出的度数.23. 综合与实践(1)、问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得 , 连接 , 以为边作等边三角形 , 则就是的平分线.
(1)、如图1,直接写出和之间的数量关系;(2)、如图2,过点作于点 , 求证:;(3)、如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分 , 平分 , 若 , , 直接写出的度数.23. 综合与实践(1)、问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得 , 连接 , 以为边作等边三角形 , 则就是的平分线.
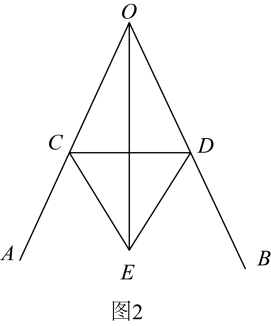
请写出平分的依据:;
(2)、类比迁移:
小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边 , 上分别取 , 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
(3)、拓展实践:
小明将研究应用于实践.如图4,校园的两条小路和 , 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
24. 下面是张老师数学课堂教学实践活动的一个片段:【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作 , . 其中 , , , . 现固定三角板 , 将三角板绕点A逆时针旋转,旋转角记为 , 射线与射线交于点P,在射线上取一点Q,使 , 连接CQ.
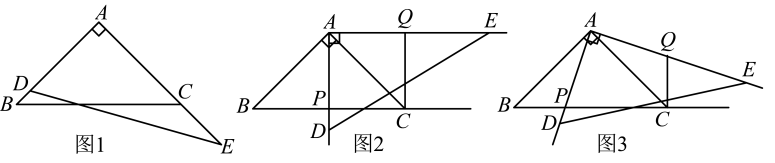 (1)、【特例探究】如图2,当时,直接写出和的数量关系和位置关系.(2)、【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.(3)、【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.(4)、【拓展应用】连接 . 若 , 的面积等于 , 请直接写出的长.
(1)、【特例探究】如图2,当时,直接写出和的数量关系和位置关系.(2)、【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.(3)、【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.(4)、【拓展应用】连接 . 若 , 的面积等于 , 请直接写出的长.