沪科版数学八年级上册第12章一次函数过关检测卷

试卷更新日期：2023-08-13 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列图象中，表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
2. 函数 $y = \sqrt{2 x - 1}$ 中自变量x的取值范围是（）

A、 $x \geq \frac{1}{2}$ B、 $x \geq - \frac{1}{2}$ C、 $x \leq - \frac{1}{2}$ D、 $x \leq \frac{1}{2}$

查看试题解析
3. 直线 $y = - x + 3$ 上有两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，且 $x_{1} < x_{2}$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法确定

查看试题解析
4. 已知一次函数 $y = k x - 3 (k \neq 0)$ ，若 $y$ 随 $x$ 的增大而减小，则它的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限

查看试题解析
5. 如图，直线 $y_{1} = k x + b$ 与直线 $y_{2} = m x - n$ 交于点 $P (1 ， a)$ ，则不等式 $m x - n - k x - b > 0$ 的解集是（）

A、 $x > 0$ B、 $x < 0$ C、 $x > 1$ D、 $x < 1$

查看试题解析
6. 一次函数 $y = k x + b$ 中，x与y的部分对应值如下表所示，则下列说法正确的是（）
$- 1$
$0$
1
2
5
2
$- 1$
$- 4$

A、x的值每增加1，y的值增加3，所以 $k = 3$ B、 $x = 2$ 是方程 $k x + b = 0$ 的解 C、函数图象不经过第四象限 D、当 $x > 1$ 时， $y < - 1$

查看试题解析
7. 无论m为何实数．直线 $y = x + 2 m$ 与 $y = - x + 4$ 的交点不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 下列表示一次函数 $y = m x - n$ 与正比例函数 $y = m n x$ （m、n为常数，且mn≠0）图象中，一定不正确的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则关于x，y的方程组 ${\begin{matrix} y = 2 x \\ y = a x + 4 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = \frac{3}{2} \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 3 \\ y = \frac{3}{2} \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
10. 甲、乙两人分别从A，B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了 $4 m i n$ ，又各自按原速前往目的地，甲、乙两人之间的距离 $y (m)$ 与甲所用时间 $x (m i n)$ 之间的函数关系如图所示．有下列说法：① $A$ ， B之间的距离为 $1200 m$ ；②乙行走的速度是甲的 $1.5$ 倍；③ $b = 800$ ；④ $a = 30$ ，以上结论正确的有 $($ $)$

A、①② B、①②③ C、①③④ D、①②④

查看试题解析

二、填空题

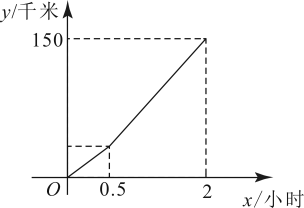
11. 已知函数 $y = (m - 1) x^{| m |} - 3$ 是关于 $x$ 的一次函数，则 $m$ 的值为.

查看试题解析
12. 一次函数的图象经过点(0，-2)，且函数y的值随自变量x的增大而增大，请写出一个符合条件的一次函数表达式．

查看试题解析
13. 已知直线 $y = k x + b$ （ $k$ ， $b$ 为常数， $k \neq 0$ ）与直线 $y = 2 x$ 平行，且与直线 $y = 3 x + 4$ 交于 $y$ 轴的同一点，则此一次函数的表达式为．

查看试题解析
14. 一辆汽车在行驶过程中，其行驶路程 $y$ （千米）与行驶时间 $x$ （小时）之间的函数关系如图所示．当 $0 \leq x \leq 0.5$ 时， $y$ 与 $x$ 之间的函数表达式为 $y = 60 x$ ；当 $0.5 \leq x \leq 2$ 时， $y$ 与 $x$ 之间的函数表达式为．

查看试题解析
15. 正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图方式放置，点A₁、A₂、A₃…和点C₁、C₂、C₃…分别在直线 $y = k x + b (k > 0)$ 和x轴上．已知点B₁（1，1）、B₂（3，2），请写出点Bn的坐标是．

查看试题解析

三、作图题

16. 通过一次函数的学习，我们积累了学习函数性质的经验和方法，请你利用所学知识来探究函数

y = | x + 1 |

的性质，解决以下问题：

(1)、填表，并画出该函数的图象.

①列表：

x	……	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4	……
y	……	3	2		0	1	2		4	5	……

②描点；

③连线.

(2)、研究函数性质：观察图象，发现函数的其中一条性质为；

(3)、观察画出的图象，当函数

y = | x + 1 |

的值大于3时，直接写出x的取值范围.

查看试题解析

四、解答题

17. 如图，一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M，

(1)、求正比例函数和一次函数的解析式；

(2)、根据图像写出使正比例函数的值大于一次函数的值的x的取值范围；

(3)、求ΔMOP的面积。

查看试题解析
18. 如图，直线 $y = k x + b$ 与x轴交于点 $A (- 5 ， 0)$ ，与y轴交于点B，与直线 $y = \frac{4}{5} x$ 交于点 $C (5 ， m)$ ．若要在y轴找到一个点P使得 $△ B P C$ 的面积为15，求这个点P的坐标．

查看试题解析

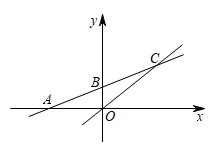
五、综合题

19. 如图，直线 $y = x + 1$ 与直线 $y = - 2 x - b$ 交于点 $P (1 ， a)$ .

(1)、求 $a$ ， $b$ 的值；

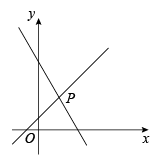(2)、方程组 ${\begin{array}{l} y = x + 1 \\ y = - 2 x - b \end{array}$ 的解为；

(3)、根据图象可得不等式 $x + 1 > - 2 x - b$ 的解集为.

查看试题解析
20. 阅读材料，回答以下问题：
我们知道，二元一次方程有无数个解，在平面直角坐标系中，我们标出以这个方程的解为坐标的点，就会发现这些点在同一条直线上．
例如 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程 $x - y = - 1$ 的一个解，对应点 $M (1 ， 2)$ ，如下图所示，我们在平面直角坐标系中将其标出，另外方程的解还有对应点 $(2 ， 3) ， (3 ， 4) \dots$ 将这些点连起来正是一条直线，反过来，在这条直线上任取一点，这个点的坐标也是方程 $x - y = - 1$ 的解．所以，我们就把条直线就叫做方程 $x - y = - 1$ 的图象．
一般的，任意二元一次方程解的对应点连成的直线就叫这个方程的图象．请问：

(1)、已知 $A (1 ， 1)$ 、 $B (- 3 ， 4)$ 、 $C (\frac{1}{2} ， 2)$ ，则点（填“A或 $B$ 或 $C$ ”）在方程 $2 x - y = - 1$ 的图象上．

(2)、求方程 $2 x + 3 y = 9$ 和方程 $3 x - 4 y = 5$ 图象的交点坐标．

(3)、已知以关于 $x 、 y$ 的方程组 ${\begin{array}{l} 5 x + 3 y = 20 + 7 m \\ 3 x + 4 y = 19 - 14 m \end{array}$ 的解为坐标的点在方程 $x + y = 5$ 的图象上，当 $t > m$ 时，化简 $\sqrt{{(- t - 2)}^{2}} - | 1 - 7 t |$ ．

查看试题解析
21. 如图，一摞相同规格的碗整齐地叠放在桌面上，桌面上碗的高度 $y （ c m ）$ 与碗数 $x$ （个）的变化情况如下表．
碗数 $x$ （个）
1
2
3
…

高度 $y （ c m ）$
5.5
          $a$
8.5
…
请根据表中给出的数据信息，解答下列问题：

(1)、上表中 $a$ 的值为；

(2)、写出叠放在桌面上碗的高度 $y （ c m ）$ 与碗数 $x$ （个）之间的关系式；

(3)、你认为这种规格的碗摞放起来的高度 $y （ c m ）$ 能达到 $18 c m$ 吗？为什么？

查看试题解析

22. 宁波市组织20辆卡车装运物资

A

，

B

，

C

三种救灾物资共100吨到灾区安置点，按计划20辆车都要装运，每辆卡车只能装运同一种救灾物资且必须装满，根据表格提供的信息，解答以下问题：

物资种类	物资 $A$	物资 $B$	物资 $C$
每辆卡车运载量（单位：吨）	6	5	4
每吨所需运费（单位：元）	120	160	100

(1)、设装运物资

A

的车辆数为

x

，装运物资

B

的车辆数为

y

，求

y

关于

x

的函数表达式；

(2)、若装运物资A的车辆数不少于5，装运物资B的车辆数不少于6，则车辆安排有哪几种方案？

(3)、在（2）的条件下，若要求总运费最少，应采取哪种方案进行运输？并求出最少运费.

查看试题解析

23. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段 $O D$ 和折线 $O A B C$ 表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

(1)、折线 $O A B C$ 表示赛跑过程中的路程与时间关系，线段 $O D$ 表示赛跑过程中的路程与时间的关系.（填“乌龟”和“兔子”）赛跑的全程是米．

(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？乌龟用了多少分钟追上了正在睡觉的兔子？

(3)、兔子醒来，以800米/分的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算一算兔子中间停下睡觉用了多少分钟？

查看试题解析

碗数 $x$ （个）	1	2	3	…
高度 $y （ c m ）$	5.5	$a$	8.5	…

		$- 1$	$0$	1	2
		5	2	$- 1$	$- 4$