2023-2024学年初中数学九年级上册 28.5 弧长和扇形面积同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，半径为4，连接OB，OC，OA，若 $∠ C A O = 40 °$ ， $∠ A C B = 70 °$ ，则阴影部分的面积是（）

A、 $\frac{4}{3} π$ B、 $\frac{8}{3} π$ C、 $\frac{16}{3} π$ D、 $\frac{32}{3} π$

查看试题解析
2. 用一个圆心角为 $90 °$ ，半径为8的扇形作一个圆锥的侧面，则这个圆锥的底面直径是（）

A、6 B、5 C、4 D、3

查看试题解析
3. 如图，把一个高 $6$ 分米的圆柱的底面分成许多相等的扇形，然后把圆柱切开，拼成一个与它等底等高的近似长方体，它的表面积比圆柱体的表面积增加了 $36$ 平方分米．原来这个圆柱的体积是立方分米．（）

A、 $105 π$ B、 $54 π$ C、 $36 π$ D、 $18 π$

查看试题解析
4. 如图，圆锥底面圆的半径为4，则这个圆锥的侧面展开图中 $\overset{⌢}{A A^{'}}$ 的长为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $16 π$

查看试题解析
5. 如图所示的曲边三角形可按下述方法作出：作等边 $△ A B C$ ；分别以点A，B，C为圆心，以AB的长为半径作 $\overset{⌢}{B C}$ ， $\overset{⌢}{A C}$ ， $\overset{⌢}{A B}$ ，三条弧所围成的图形就是一个曲边三角形．如果 $A B = 3$ ，那么这个曲边三角形的周长是（）．

A、π B、 $2 π$ C、 $\frac{9}{2} π$ D、 $3 π$

查看试题解析
6. 已知在扇形 $O A B$ 中， $∠ A O B = 90 °$ ， $O B = 4$ ， $C$ 为弧 $A B$ 的中点， $D$ 为半径 $O B$ 上一动点，点 $B$ 关于直线 $C D$ 的对称点为 $M$ ，若点 $M$ 落在扇形 $O A B$ 内 $($ 不含边界 $)$ ，则 $O D$ 长的取值范围是（）

A、 $4 \sqrt{2} - 4 < O D < 2 \sqrt{2}$ B、 $2 \sqrt{2} < O D < 4 \sqrt{2}$ C、 $0 < O D < 2 \sqrt{2}$ D、 $4 - 2 \sqrt{2} < O D < 4$

查看试题解析
7. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点 $M$ 、 $N$ 分别是边 $A D$ 、 $B C$ 的中点，某一时刻，动点 $E$ 从点 $M$ 出发，沿 $M A$ 方向以每秒2个单位长度的速度向点 $A$ 匀速运动；同时，动点 $F$ 从点 $N$ 出发，沿 $N C$ 方向以每秒1个单位长度的速度向点 $C$ 匀速运动，其中一点运动到矩形顶点时，两点同时停止运动，连接 $E F$ ，过点 $B$ 作 $E F$ 的垂线，垂足为 $H$ .在这一运动过程中，点 $H$ 所经过的路径长是（）

A、 $\frac{\sqrt{5}}{2} π$ B、 $\sqrt{5} π$ C、 $\sqrt{2} π$ D、 $2 \sqrt{2} π$

查看试题解析
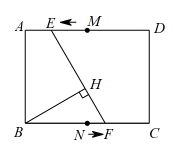8. 扇形的半径是100厘米，圆心角为18°，下列计算错误的是（）。

A、弧长l=31.4厘米 B、扇形面积S=1570平方厘米 C、扇形周长为131.4厘米 D、所在圆的面积为31400平方厘米

查看试题解析

二、填空题

9. 如图，一个圆桶底面直径为5cm，高12cm，则桶内所能容下的最长木棒为cm.

查看试题解析
10. 如图，正八边形 $A B C D E F G H$ 的边长为4，以顶点A为圆心， $A B$ 的长为半径画圆，则阴影部分的面积为（结果保留 $π$ ）．

查看试题解析
11. 如图，在扇形 $O B A$ 中， $∠ A O B = 9 0^{°} ， C ， D$ 分别是OA，OB的中点，连接AD和BC交于点 $E$ ，若 $O A = 2$ ，则图中阴影部分的面积为.

查看试题解析
12. 如图，△ABC中，∠ACB＝90°，AC＝6，BC＝8，P为△ABC外以AB为直径的半圆上一动点，当点P从点A运动到点B时，线段CP的中点Q运动的路线长为.

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B$ =6， $B C$ =8，点 $M$ 、 $N$ 分别是边 $A D$ 、 $B C$ 的中点，某一时刻，动点 $E$ 从点 $M$ 出发，沿 $M A$ 方向以每秒2个单位长度的速度向点 $A$ 匀速运动；同时，动点 $F$ 从点 $N$ 出发，沿 $N C$ 方向以每秒1个单位长度的速度向点 $C$ 匀速运动，其中一点运动到矩形顶点时，两点同时停止运动，连接 $E F$ ，过点 $B$ 作 $E F$ 的垂线，垂足为 $H$ .在这一运动过程中，点 $H$ 所经过的路径长是.

查看试题解析

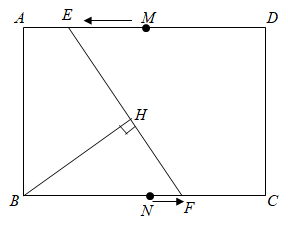
三、解答题

14. 求阴影部分的周长：

(1)、

(2)、

查看试题解析
15. 弯制管道时，先按中心计算“展直长度”再下料，试计算图中所示管道的展直长度。（π≈3.14，单位：cm，精确到1cm，弯制管道的粗细不计）

查看试题解析

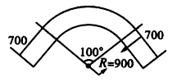
四、综合题

16. 在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动
【问题情境】

刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：

如图，将一个三角形纸板 $△ A B C$ 绕点A逆时针旋转 $θ$ 到达 $△ A B^{'} C^{'}$ 的位置，那么可以得到：

$A B = A B^{'} ， A C = A C^{'} ， B C = B^{'} C^{'}$ ； $∠ B A C = ∠ B^{'} A C^{'} ， ∠ A B C = ∠ A B^{'} C^{'} ， ∠ A C B = ∠ A C^{'} B^{'}$ （）

刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键故数学就是一门哲学．

(1)、【问题解决】
上述问题情境中“（）”处应填理由：；

(2)、如图，小王将一个半径为 $4 c m$ ，圆心角为 $60 °$ 的扇形纸板ABC绕点O逆时针旋转 $90 °$ 到达扇形纸板 $A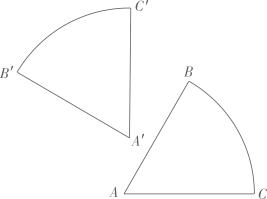^{'} B^{'} C^{'}$ 的位置．

①请在图中作出点O；

②如果 $B B^{'} = 6 c m$ ，则在旋转过程中，点B经过的路径长为；

(3)、【问题拓展】小李突发奇想，将与（2）中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置另一个在孤的中点处固定，然后放开纸板，使其摆动到竖直位置时静止此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．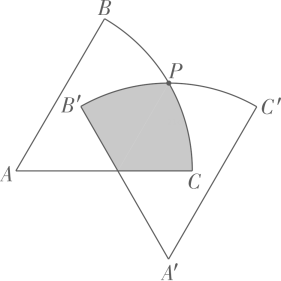

查看试题解析
17. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (0 ， 3)$ ， $B (3 ， 4)$ ， $C (2 ， 2)$ ，将 $△ A B C$ 向左平移3个单位长度，再向下平移4个单位长度得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标；

(2)、画出将 $△ A_{1} B_{1} C_{1}$ 绕点O按逆时针方向旋转 $90 °$ 后的图形 $△ A_{2} B_{2} C_{2}$ ；

(3)、求 $△ A_{1} B_{1} C_{1}$ 在旋转过程中扫过的面积．

查看试题解析

2023-2024学年初中数学九年级上册 28.5 弧长和扇形面积 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 28.5 弧长和扇形面积同步分层训练培优卷(冀教版)