2023-2024学年初中数学九年级上册 28.4 垂径定理 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,是的弦,于点 , 若 , , 则弦的长为( )
 A、4 B、 C、 D、2. 如图,是的弦,交于点C,点D是优弧上一点,若 , 则( )
A、4 B、 C、 D、2. 如图,是的弦,交于点C,点D是优弧上一点,若 , 则( ) A、 B、 C、 D、3. 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
A、 B、 C、 D、3. 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( ) A、 B、 C、 D、4. 下列命题正确的是( )A、三点确定一个圆 B、圆的任意一条直径都是它的对称轴 C、等弧所对的圆心角相等 D、平分弦的直径垂直于这条弦5. 如图,小明分别以点A, B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,作直线EF分别交弦AB和劣弧AB于点C, D.小明量得AB=4cm, CD=1cm.则劣弧AB所在圆的半径长为( )
A、 B、 C、 D、4. 下列命题正确的是( )A、三点确定一个圆 B、圆的任意一条直径都是它的对称轴 C、等弧所对的圆心角相等 D、平分弦的直径垂直于这条弦5. 如图,小明分别以点A, B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,作直线EF分别交弦AB和劣弧AB于点C, D.小明量得AB=4cm, CD=1cm.则劣弧AB所在圆的半径长为( ) A、3cm B、2.5cm C、2cm D、2.4cm6. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深等于1寸,锯道长1尺,则圆形木材的直径是( )(1尺=10寸)
A、3cm B、2.5cm C、2cm D、2.4cm6. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深等于1寸,锯道长1尺,则圆形木材的直径是( )(1尺=10寸) A、12寸 B、13寸 C、24寸 D、26寸7. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( )
A、12寸 B、13寸 C、24寸 D、26寸7. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( ) A、5 B、18 C、3 D、178. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
A、5 B、18 C、3 D、178. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:①AD2+AC2=4;②∠DBC+∠ADO=90°;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
其中正确的是( )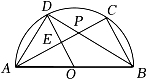 A、①②③ B、②③④ C、③④ D、②④
A、①②③ B、②③④ C、③④ D、②④二、填空题
-
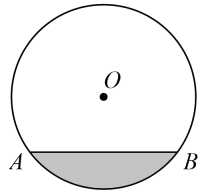
9. 如图,是一个盛有水的容器的横截面,的半径为 . 水的最深处到水面的距离为 , 则水面的宽度为 .
 10. 如图,在以O为圆心半径不同的两个圆中,大圆和小圆的半径分别为6和4,大圆的弦交小圆于点C , D . 若 , 则的长为 .
10. 如图,在以O为圆心半径不同的两个圆中,大圆和小圆的半径分别为6和4,大圆的弦交小圆于点C , D . 若 , 则的长为 . 11. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 .
11. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 . 12. 在平面直角坐标系中,我们定义点的“关联点”为 . 如果已知点在直线上,点在的内部,的半径长为(如图所示),那么点的横坐标的取值范围是 .
12. 在平面直角坐标系中,我们定义点的“关联点”为 . 如果已知点在直线上,点在的内部,的半径长为(如图所示),那么点的横坐标的取值范围是 . 13. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 , 以点A为圆心,3为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与交于点K,连结HG、CH.给出下列四个结论.(1)H是FK的中点;(2);(3);(4) , 其中正确的结论有(填写所有正确结论的序号).
13. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 , 以点A为圆心,3为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与交于点K,连结HG、CH.给出下列四个结论.(1)H是FK的中点;(2);(3);(4) , 其中正确的结论有(填写所有正确结论的序号).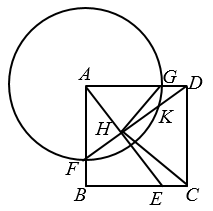
三、解答题
-
14. 随着疫情的持续,各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的,图形下面是长方形ABCD,上面是半圆形,其中 , , 一辆装满货物的运输车,其外形高2.6m,宽2.4m,它能通过储藏室的门吗?请说明理由.
 15. 如图,是的直径,弦于点E, , 若 , 求的长.
15. 如图,是的直径,弦于点E, , 若 , 求的长.
四、综合题

