2023-2024学年初中数学九年级上册 28.4 垂径定理 同步分层训练基础卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 下列命题是假命题的是( )A、两条平行线间的距离处处相等 B、平分弦的直径垂直于弦 C、正方形的两条对角线互相垂直平分 D、在同圆或等圆中,同弧或等弧所对的圆周角相等2. 如图,已知是的一条弦, , 点M在上,且 , 若 , 则⊙O的半径为( )
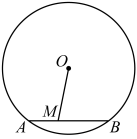 A、4 B、5 C、6 D、3. 下列语句中不正确的有( )
A、4 B、5 C、6 D、3. 下列语句中不正确的有( )①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤圆内接四边形的对角互补.
A、5个 B、4个 C、3个 D、2个4. 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( ) A、2 B、 C、2 D、35. 下列图形中的角是圆周角的是( )A、
A、2 B、 C、2 D、35. 下列图形中的角是圆周角的是( )A、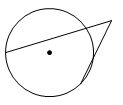 B、
B、 C、
C、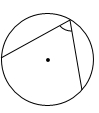 D、
D、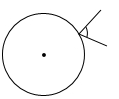 6. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( )
6. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( ) A、8 B、4 C、3.5 D、37. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( )
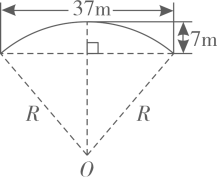
A、8 B、4 C、3.5 D、37. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( ) A、 B、 C、 D、8. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
A、 B、 C、 D、8. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,的弦 , 过点O作于点C,交于点P,若 , 则的半径为.
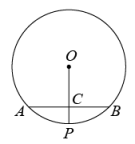 10. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .
10. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .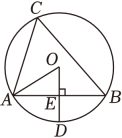 11. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数)
11. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数) 12. 水平放置的圆柱形油槽的圆形截面如图2所示,如果该截面油的最大深度为分米,油面宽度为分米,那么该圆柱形油槽的内半径为分米.
12. 水平放置的圆柱形油槽的圆形截面如图2所示,如果该截面油的最大深度为分米,油面宽度为分米,那么该圆柱形油槽的内半径为分米. 13. 如图,已知的内接正方形 , 点是的中点,与边交于点 , 那么 .
13. 如图,已知的内接正方形 , 点是的中点,与边交于点 , 那么 .
三、解答题
-
14. 《九章算术》标志中国古代数学形成了完整的体系,第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表述为:“如图,是的直径,弦于点 , 寸,寸,求直径的长,”请你解答这个问题.
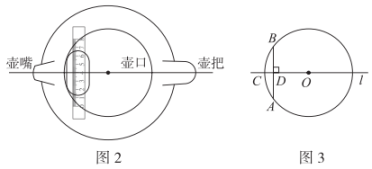
 15. 紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1。当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是符合题意使用该工具时的示意图.如图3,为某紫砂壶的壶口,已知 , 两点在上,直线过点 , 且于点 , 交于点 . 若 , , 求这个紫砂壶的壶口半径的长.
15. 紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1。当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是符合题意使用该工具时的示意图.如图3,为某紫砂壶的壶口,已知 , 两点在上,直线过点 , 且于点 , 交于点 . 若 , , 求这个紫砂壶的壶口半径的长.
四、作图题
-
16. 如图,在中, , .

尺规作图:
(1)、在线段上求作一点 , 使;②连接 , 以点为圆心,的长为半径画弧,交的延长线于点 , 连接.(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求的度数;(3)、在(1)的条件下,若 , 求的周长.五、综合题