2023-2024学年初中数学九年级上册 28.3 圆心角和圆周角 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,是的直径, , 则等于( )
 A、32° B、58° C、60° D、64°2. 如图,是的直径,是上任意一点(不与 , 重合),设 , , 所对的边分别为 , , , 则( )
A、32° B、58° C、60° D、64°2. 如图,是的直径,是上任意一点(不与 , 重合),设 , , 所对的边分别为 , , , 则( ) A、 B、 C、 D、3. 如图,在正方形中,以边为直径在其内部作半圆,F是半圆上一点,连接 , , 过点D作于点E,点G是线段ED上一点, , 连接并延长交于点P,则的值是( )
A、 B、 C、 D、3. 如图,在正方形中,以边为直径在其内部作半圆,F是半圆上一点,连接 , , 过点D作于点E,点G是线段ED上一点, , 连接并延长交于点P,则的值是( ) A、 B、 C、 D、4. 如图,是的直径,点C、D在上,且在两侧,于点H交线段于E.若 , , , 则的长为( )
A、 B、 C、 D、4. 如图,是的直径,点C、D在上,且在两侧,于点H交线段于E.若 , , , 则的长为( )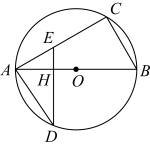 A、 B、 C、 D、5. 如图,在中,是直径,弦的长为5,点D在圆上,且 , 则的半径为( )
A、 B、 C、 D、5. 如图,在中,是直径,弦的长为5,点D在圆上,且 , 则的半径为( ) A、2.5 B、5 C、7.5 D、106. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )
A、2.5 B、5 C、7.5 D、106. 如图,在中,以为直径的分别与交于点F,D,点F是的中点,连接交于点E.若 . 连接 , 则弦的长为( )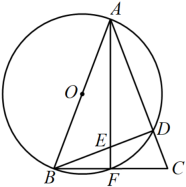 A、 B、 C、4 D、57. 如图,已知四边形两条对角线相交于点 , , , , 则的值为( )
A、 B、 C、4 D、57. 如图,已知四边形两条对角线相交于点 , , , , 则的值为( ) A、6 B、7 C、12 D、168. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )
A、6 B、7 C、12 D、168. 如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , .
 10. 如图,点A,B,C在上, , 则等于 °.
10. 如图,点A,B,C在上, , 则等于 °.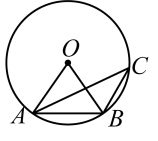 11. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .12. 如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①CEF∽ACD;②=2;③sin∠CAD=;④AB=BF.其中正确的结论有(写出所有正确结论的序号).
11. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .12. 如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①CEF∽ACD;②=2;③sin∠CAD=;④AB=BF.其中正确的结论有(写出所有正确结论的序号). 13. 如图,四边形ABCD内接于以BD为直径的⊙O,CA平分∠BCD,若四边形ABCD的面积是30cm2 , 则AC=cm.
13. 如图,四边形ABCD内接于以BD为直径的⊙O,CA平分∠BCD,若四边形ABCD的面积是30cm2 , 则AC=cm.
三、解答题
-
14. 如图,已知四边形内接于.求证:.
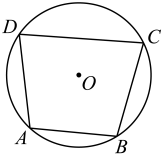 15. 如图,的直径 , 、是圆上的两点, , , 求 , 两点的距离.
15. 如图,的直径 , 、是圆上的两点, , , 求 , 两点的距离.
四、综合题
-
16. 如图1,C、D是以为直径的上的点,且满足 , 点P在上,交于点M,交于点G,交于点N,交于点H.
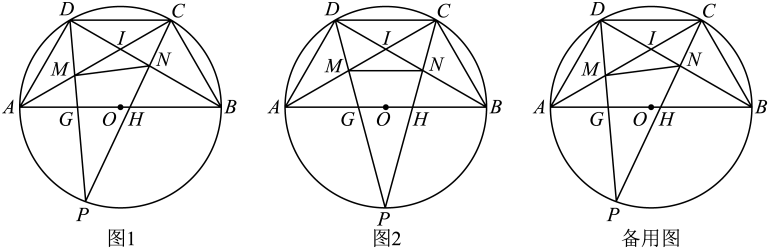 (1)、求的度数.(2)、如图2,当点P是的中点时,
(1)、求的度数.(2)、如图2,当点P是的中点时,①求证:是等腰三角形.
②求的值.
(3)、如图1,设 , 与的面积差为y,求y关于x的函数表达式.17. 如图1,在平面直角坐标系中,O为坐标原点,是等腰直角三角形,点A,点B在x轴上(点A在点B的左侧),点C在y轴的正半轴上,点D在直线BC上运动,连结AD与y轴交于点E,连结BE. (1)、当点D从点C运动到点B(C,B两点除外)时,求证:.(2)、如图2,过B,D,E三点作⊙H与y轴的另一个交点为G,延长EH交⊙H于点F,连结GF,DG,BF.求的度数.(3)、在(2)的条件下,若 , 点D在运动过程中,中是否有一个角等于 , 如果存在,求出此时点E的坐标;如果不存在,请说明理由.
(1)、当点D从点C运动到点B(C,B两点除外)时,求证:.(2)、如图2,过B,D,E三点作⊙H与y轴的另一个交点为G,延长EH交⊙H于点F,连结GF,DG,BF.求的度数.(3)、在(2)的条件下,若 , 点D在运动过程中,中是否有一个角等于 , 如果存在,求出此时点E的坐标;如果不存在,请说明理由.