2023-2024学年初中数学九年级上册 28.3 圆心角和圆周角 同步分层训练基础卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,是的直径,点C,D在上,连接 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 如图,已知是的直径,内接于 , 若 , , 则的值为( )
A、 B、 C、 D、2. 如图,已知是的直径,内接于 , 若 , , 则的值为( ) A、 B、 C、 D、3. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半4. 学了圆后,小亮突发奇想,想到用这种方法测量三角形的角度:将三角形纸片如图1放置,使得顶点C在量角器的半圆上,纸片另外两边分别与量角器交于A,B两点.点A,B的度数是 , , 这样小明就能得到的度数.请你帮忙算算的度数是( )
A、 B、 C、 D、3. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半4. 学了圆后,小亮突发奇想,想到用这种方法测量三角形的角度:将三角形纸片如图1放置,使得顶点C在量角器的半圆上,纸片另外两边分别与量角器交于A,B两点.点A,B的度数是 , , 这样小明就能得到的度数.请你帮忙算算的度数是( ) A、 B、 C、 D、5. 如图,已知 是 的直径, 切 于点A, .则下列结论中不一定正确的是( )
A、 B、 C、 D、5. 如图,已知 是 的直径, 切 于点A, .则下列结论中不一定正确的是( ) A、 B、 C、 D、6. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法.如《淮南子天文训》中记载:“正朝夕:先树一表东方;操一表却去前表十步,以参望日始出北廉.日直入,又树一表于东方,因西方之表,以参望日方入北康.则定东方两表之中与西方之表,则东西也.”如图,用几何语言叙述作图方法:已知直线a和直线外一定点O,过点O作直线与a平行.(1)以O为圆心,单位长为半径作圆,交直线a于点M,N;(2)分别在的延长线及上取点A,B,使;(3)连接 , 取其中点C,过O,C两点确定直线b,则直线 . 按以上作图顺序,若 , 则( )
A、 B、 C、 D、6. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法.如《淮南子天文训》中记载:“正朝夕:先树一表东方;操一表却去前表十步,以参望日始出北廉.日直入,又树一表于东方,因西方之表,以参望日方入北康.则定东方两表之中与西方之表,则东西也.”如图,用几何语言叙述作图方法:已知直线a和直线外一定点O,过点O作直线与a平行.(1)以O为圆心,单位长为半径作圆,交直线a于点M,N;(2)分别在的延长线及上取点A,B,使;(3)连接 , 取其中点C,过O,C两点确定直线b,则直线 . 按以上作图顺序,若 , 则( ) A、 B、 C、 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )
A、 B、 C、 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )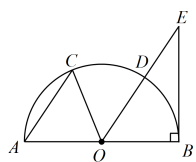 A、 B、 C、 D、8. 下列说法中正确的说法有( )个
A、 B、 C、 D、8. 下列说法中正确的说法有( )个①对角线相等的四边形是矩形②在同圆或等圆中,同一条弦所对的圆周角相等③相等的圆心角所对的弧相等④平分弦的直径垂直于弦,并且平分弦所对的弧⑤到三角形三边距离相等的点是三角形三个内角平分线的交点
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,在 中, , ,则图中阴影部分的面积为.
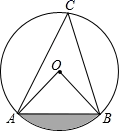 10. 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接 , 则的度数为 .
10. 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接 , 则的度数为 .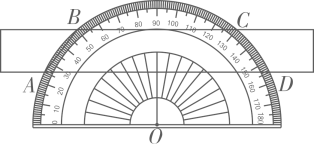 11. 如图,四边形内接于 , 的延长线相交于点E,的延长线相交于点F.若 , , 则°.
11. 如图,四边形内接于 , 的延长线相交于点E,的延长线相交于点F.若 , , 则°. 12. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是 , 为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器台.
12. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是 , 为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器台.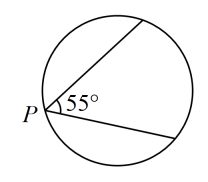 13. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.
13. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.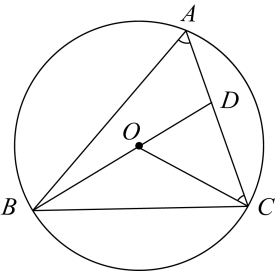
三、解答题
-
14. 如图,是的内接三角形,点D是的中点,弦交于点E.与相似吗?为什么?
 15. 如图,O是半圆的圆心,C、E是圆上的两点, , , .求证:.
15. 如图,O是半圆的圆心,C、E是圆上的两点, , , .求证:.
四、作图题
-
16. 如图是由小正方形组成的网格,每个小正方形的顶点叫作格点已知的圆心在格点上,圆上 , 两点均在格线上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
 (1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .
(1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .五、综合题

