2023-2024学年初中数学九年级上册 28.2 过三点的圆 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
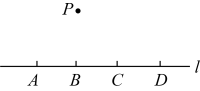 A、3个 B、4个 C、5个 D、6个2. 如图,在已知的△ABC中,按以下步骤:(1)分别以B、C为圆心,大于BC的长为半径作弧,两弧相交M、N;(2)作直线MN,交AB于D,连接CD,若CD=AD,∠B=25°,则下列结论中错误的是( )
A、3个 B、4个 C、5个 D、6个2. 如图,在已知的△ABC中,按以下步骤:(1)分别以B、C为圆心,大于BC的长为半径作弧,两弧相交M、N;(2)作直线MN,交AB于D,连接CD,若CD=AD,∠B=25°,则下列结论中错误的是( ) A、直线MN是线段BC的垂直平分线 B、点D为△ABC的外心 C、∠ACB=90° D、点D为△ABC的内心3. 如图,是的直径,点C,D在上,若 , 则的度数是( )
A、直线MN是线段BC的垂直平分线 B、点D为△ABC的外心 C、∠ACB=90° D、点D为△ABC的内心3. 如图,是的直径,点C,D在上,若 , 则的度数是( ) A、40° B、45° C、50° D、80°4. 如图,是的外接圆,是的直径,点在上,若的半径为6, , 则的长度为( )
A、40° B、45° C、50° D、80°4. 如图,是的外接圆,是的直径,点在上,若的半径为6, , 则的长度为( )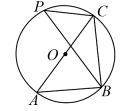 A、3 B、 C、 D、65. 如图,是等边的外接圆,若 , 则的半径是( )
A、3 B、 C、 D、65. 如图,是等边的外接圆,若 , 则的半径是( ) A、 B、 C、 D、6. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个7. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )
A、 B、 C、 D、6. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个7. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )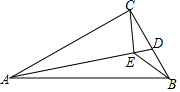 A、1 B、 C、2 D、8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( )
A、1 B、 C、2 D、8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( ) A、72 B、96 C、120 D、144
A、72 B、96 C、120 D、144二、填空题
-
9. 如图,内接于圆O.若 , , , 则的弧长为 .
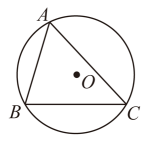 10. 如图,是的外接圆, , , 则的直径为 .
10. 如图,是的外接圆, , , 则的直径为 .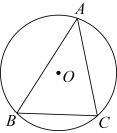 11. 如图,四边形为正方形,的平分线交于点E,将绕点B顺时针旋转90°得到 , 延长交于点G,连接 , , 与相交于点H.有下列结论:①;②G为的外心;③;④ . 其中正确结论的序号是 .
11. 如图,四边形为正方形,的平分线交于点E,将绕点B顺时针旋转90°得到 , 延长交于点G,连接 , , 与相交于点H.有下列结论:①;②G为的外心;③;④ . 其中正确结论的序号是 . 12. 已知点 ,原点O关于一次函数 的对称点 恰好与 的外心重合,则点 的坐标为 , b的值为 .13. 在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,若“心形”图形的顶点A,B,C,D,E,F,G均为整点,已知点P(3,4),线段PQ的长为 , PQ关于过点M(0,5)的直线l对称得到P'Q',点P的对应点为P′,当点P′恰好落在“心形”图形边的整点上时,点Q'也落在“心形”图形边的整点上,则这样的点Q′共有 个.
12. 已知点 ,原点O关于一次函数 的对称点 恰好与 的外心重合,则点 的坐标为 , b的值为 .13. 在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,若“心形”图形的顶点A,B,C,D,E,F,G均为整点,已知点P(3,4),线段PQ的长为 , PQ关于过点M(0,5)的直线l对称得到P'Q',点P的对应点为P′,当点P′恰好落在“心形”图形边的整点上时,点Q'也落在“心形”图形边的整点上,则这样的点Q′共有 个.
三、作图题
-
14. 如图是由边长为的小正方形构成的网格.每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示.画图结果用实线表示,完成下列问题:

⑴ ▲ ;
⑶将边绕点顺时针旋转得到线段则 ▲ ;
⑶画出的外接圆的圆心;
⑷在上确定一点 , 使 .
四、综合题
-
15. 在△ABC中,AC=BC=5,tanA= , E分别是AB,AC边上的动点,作△ADE关于DE对称的图形△A′DE.
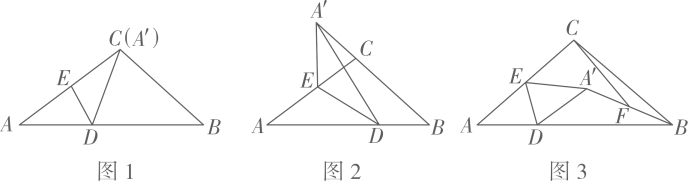 (1)、如图1,当点A′恰好与点C重合,求DE的长;(2)、如图2,当点A’落在BC的延长线上,且A’E⊥AB,求AD的长;(3)、如图3,若AE=CE,连接A’B,F是A’B的中点,连接CF,在D点的运动过程中,求线段CF长度的最大值.16. 八上教材给出了命题“如果 , , 分别是 和 的高,那么 ”的证明,由此进一步思考……
(1)、如图1,当点A′恰好与点C重合,求DE的长;(2)、如图2,当点A’落在BC的延长线上,且A’E⊥AB,求AD的长;(3)、如图3,若AE=CE,连接A’B,F是A’B的中点,连接CF,在D点的运动过程中,求线段CF长度的最大值.16. 八上教材给出了命题“如果 , , 分别是 和 的高,那么 ”的证明,由此进一步思考……(问题提出)
(1)、在 和 中, , 分别是 和 的高,如果 , , ,那么 和 全等吗?(i)小红的思考
如图,先任意画出一个 ,然后按下列作法,作出一个满足条件的 ,作法如下:

①作 的外接圆
②过点 作 ,与 交于点
③连接 (点 与 重合), (点 与 重合),得到
请说明小红所作的 .
(ii)小明的思考
如图,对于满足条件的 , 和高 , ;小明将 通过图形的变换,使边 与 重合, , 相交于点 ,连接 ,易证

接下来,小明的证明途径可以用下面的框图表示,请填写其中的空格.
 (2)、小明解决了问题(1)后,继续探索,提出了下面的问题,请你证明.
(2)、小明解决了问题(1)后,继续探索,提出了下面的问题,请你证明.如图,在 和 中, , 分别是 和 的高,( ),且 , ,求证: .

-