2023-2024学年初中数学九年级上册 28.1 圆的概念和性质同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $A B$ 是半圆 $O$ 的直径，四边形 $C D M N$ 和 $D E F G$ 都是正方形，其中点 $C$ ， $D$ ， $E$ 在 $A B$ 上，点 $F$ ， $N$ 在半圆上.若半圆 $O$ 的半径为10，则正方形 $C D M N$ 的面积与正方形 $D E F G$ 的面积之和是（）

A、50 B、75 C、100 D、125

查看试题解析
2. 如图，已知OA，OB， OC是⊙O的半径，连结BC，交OA于点D，设∠ADB=a，∠OBC=p，∠AOC=y，则（）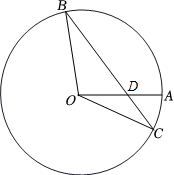

A、a+2β-y= 180° B、a+β+y= 180° C、2a-β+y=180° D、3a-2β+y=180°

查看试题解析
3. 下列4个说法中，正确的有（）
①直径是弦 ②弦是直径 ③任何一条直径所在的直线都是圆的对称轴 ④弧是半圆

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列说法中，正确的是（）

A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、直径未必是弦

查看试题解析
5. 如图，圆上有两点 $A$ ， $B$ ，连结 $A B$ ，分别以 $A$ ， $B$ 为圆心， $A B$ 的长为半径画弧，两弧相交于点 $C ， D ， C D$ 交于 $A B$ 点E，交 $\overset{⌢}{A B}$ 于点F，若 $E F = 1 ， A B = 6$ ，则该圆的半径长是（）

A、10 B、6 C、5 D、4

查看试题解析
6. 如图是一个半径为6cm的 $⊙ O$ 的纸片， $△ A B C$ 是 $⊙ O$ 的内接三角形，分别以直线 $A B$ 和 $A C$ 折叠 $⊙ O$ 纸片， $\overset{⌢}{A B}$ 和 $\overset{⌢}{A C}$ 都经过圆心O，则图中阴影部分的面积是（）

A、 $9 \sqrt{3} c m^{2}$ B、 $8 \sqrt{3} c m^{2}$ C、 $9 \sqrt{6} c m^{2}$ D、 $12 c m^{2}$

查看试题解析
7. 如图是一个半径为6cm的 $⊙ O$ 的纸片， $△ A B C$ 是 $⊙ O$ 的内接三角形，分别以直线 $A B$ 和 $A C$ 折叠 $⊙ O$ 纸片， $\overset{⌢}{A B}$ 和 $\overset{⌢}{A C}$ 都经过圆心O，则图中阴影部分的面积是（）

A、 $9 \sqrt{3} c m^{2}$ B、 $8 \sqrt{3} c m^{2}$ C、 $9 \sqrt{6} c m^{2}$ D、 $12 c m^{2}$

查看试题解析
8. 如图，在 $⊙ O$ 中， $AB$ 是直径， $AC$ 是弦，连接 $OC$ ，若 $∠ ACO = 25 °$ ，则 $∠ BOC$ 的度数是（）

A、 $40 °$ B、 $50 °$ C、 $55 °$ D、 $60 °$

查看试题解析

二、填空题

9. 如图，点A、B、C在 $⊙ O$ 上，且 $A C ∥ O B$ ，若 $∠ B O C = 42 °$ ，则 $∠ A O C$ 的度数为 $^{∘}$ .

查看试题解析
10. 在同一平面内，点P到 $⊙ O$ 的最长距离为 $8 c m$ ，最短距离为 $2 c m$ ，则 $⊙ O$ 的半径为.

查看试题解析
11. 在 $△ A B C$ 中， $A B = 4 \sqrt{3}$ ， $∠ C = 60 °$ ，在边 $B C$ 上有一点 $P$ ，且 $B P = \frac{1}{2} A C$ ，连接 $A P$ ，则 $A P$ 的最小值为．

查看试题解析
12. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖 $\overset{⌢}{M N}$ 与两个磁体组成（下侧磁体固定不动），连接杆 $E F$ 与地面 $B D$ 垂直，排水口 $C D = 24 \sqrt{3} m m$ ，密封盖最高点E到地面的距离为 $6 m m$ ，整个地漏的高度 $E G = 75 m m$ （G为磁体底部中点），密封盖被磁体顶起将排水口密封， $\overset{⌢}{M N}$ 所在圆的半径为 $m m$ ；当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点 $M^{'}$ 恰好落在 $B G$ 中点，若点 $M^{'}$ 到 $E^{'} F^{'}$ 的距离为 $36 m m$ ，则密封盖下沉的最大距离为 $m m$ .

查看试题解析
13. 如图，在Rt△ABC与Rt△AEF中，CD为∠ACB的角平分线，且∠ACB=30°，AE=EF=2，AB= $\frac{\sqrt{6} + \sqrt{2}}{2}$ ，现将△AEF绕点A顺时针旋转，在旋转过程中，当△FDC的面积最大时，则点F到直线CD的距离为.

查看试题解析

三、解答题

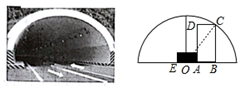
14. 某隧道施工单位准备在双向道路中间全程增加一个宽为1米的隔离带，已知隧道截面是一个半径为4米的半圆形，点O是其圆心，AE是隔离带截面，问一辆高3米，宽1.9米的卡车ABCD能通过这个隧道吗？请说明理由．

查看试题解析
15.
如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（-4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．

（1）求直线AB的函数解析式；
（2）当点P在线段AB（不包括A，B两点）上时．
①求证：∠BDE=∠ADP；
②设DE=x，DF=y．请求出y关于x的函数解析式；
（3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．

查看试题解析

四、综合题

16. 下面是小东设计的“以线段AB为一条对角线作一个菱形”的尺规作图过程．
已知：线段AB．

求作：菱形ACBD．

作法：如图，

①以点A为圆心，以AB长为半径作⊙A；

②以点 B为圆心，以AB长为半径作⊙B，

交⊙A 于C，D两点；

③连接AC，BC，BD，AD．

所以四边形ACBD就是所求作的菱形．

根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵点B，C，D在⊙A上，

∴AB=AC=AD(      ▲       )（填推理的依据）．

同理 ∵点A，C，D在⊙B上，

∴AB=BC=BD．

∴    ▲    =   ▲    =   ▲    =    ▲    ．

∴四边形ACBD是菱形． (     ▲     )（填推理的依据）．

查看试题解析
17. 在平面直角坐标系 $x O y$ 中，⊙O的半径为1，A，B为⊙O外两点，AB=1．给出如下定义：平移线段AB，得到⊙O的弦 $A^{'} B^{'}$ （ $A^{'} ， B^{'}$ 分别为点A，B的对应点），线段 $A A^{'}$ 长度的最小值称为线段AB到⊙O的“平移距离”．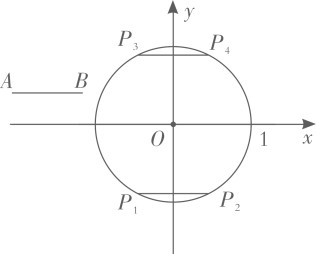

(1)、如图，平移线段AB到⊙O的长度为1的弦 $P_{1} P_{2}$ 和 $P_{3} P_{4}$ ，则这两条弦的位置关系是；在点 $P_{1} ， P_{2} ， P_{3} ， P_{4}$ 中，连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”；

(2)、若点A，B都在直线 $y = \sqrt{3} x + 2 \sqrt{3}$ 上，记线段AB到⊙O的“平移距离”为 $d_{1}$ ，求 $d_{1}$ 的最小值；

(3)、若点A的坐标为 $(2 ， \frac{3}{2})$ ，记线段AB到⊙O的“平移距离”为 $d_{2}$ ，直接写出 $d_{2}$ 的取值范围．

查看试题解析

2023-2024学年初中数学九年级上册 28.1 圆的概念和性质 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 28.1 圆的概念和性质同步分层训练培优卷(冀教版)