2023-2024学年初中数学九年级上册 28.1 圆的概念和性质 同步分层训练基础卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出米的螺旋曲线.在平面直角坐标系中,依次以这组数为半径作的圆弧 , 得到一组螺旋线,连接 , 得到一组螺旋折线,如图所示.已知点的坐标分别为 , 则点的坐标为( )
 A、 B、 C、 D、2. 如图,为的直径,是的弦,、的延长线交于点E,已知 , , 则的度数为( )
A、 B、 C、 D、2. 如图,为的直径,是的弦,、的延长线交于点E,已知 , , 则的度数为( ) A、 B、 C、 D、3. 下列图形中,称为扇形的是( )A、
A、 B、 C、 D、3. 下列图形中,称为扇形的是( )A、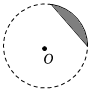 B、
B、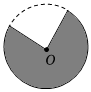 C、
C、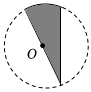 D、
D、 4. 在平面内与点的距离为1cm的点的个数为( )A、无数个 B、3个 C、2个 D、1个5. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
4. 在平面内与点的距离为1cm的点的个数为( )A、无数个 B、3个 C、2个 D、1个5. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).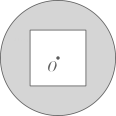 A、 B、2 C、 D、6. 如图是两个大小不同的量角器.小量角器由于长时间使用,某些刻度已经模糊不清.现将两个量角器的零刻度线放在同一直线上,使与C重合(如下图).如果两个半圆的公共点P在大量角器上对应的度数为 , 那么在小量角器上对应的度数为( )
A、 B、2 C、 D、6. 如图是两个大小不同的量角器.小量角器由于长时间使用,某些刻度已经模糊不清.现将两个量角器的零刻度线放在同一直线上,使与C重合(如下图).如果两个半圆的公共点P在大量角器上对应的度数为 , 那么在小量角器上对应的度数为( ) A、 B、 C、 D、7. 如图,在中, , 则劣弧的度数为( )
A、 B、 C、 D、7. 如图,在中, , 则劣弧的度数为( )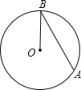 A、106° B、126° C、74° D、53°8. 如图,在中,点D,E分别是的中点,以点A为圆心,为半径作圆弧交于点F.若 , , 则的长为( )
A、106° B、126° C、74° D、53°8. 如图,在中,点D,E分别是的中点,以点A为圆心,为半径作圆弧交于点F.若 , , 则的长为( ) A、2 B、2.5 C、3 D、3.5
A、2 B、2.5 C、3 D、3.5二、填空题
-
9. 如图,分别以数轴的单位长度1和3为直角边的长作直角三角形,以数轴上的原点O为圆心,这个直角三角形的斜边长为半径作弧与数轴交于一点A,则点A表示的数为
 10. 如图,点A,B,C在⊙O上, , , 则.
10. 如图,点A,B,C在⊙O上, , , 则. 11. 如图,在平面直角坐标系中, 点A的坐标为 , 点B的坐标为 , 点为轴上方一动点,且 , 以点为直角顶点构造等腰直角三角形 , 当线段取最大值时, , 点的坐标为.
11. 如图,在平面直角坐标系中, 点A的坐标为 , 点B的坐标为 , 点为轴上方一动点,且 , 以点为直角顶点构造等腰直角三角形 , 当线段取最大值时, , 点的坐标为. 12. 如图,数学知识在生产和生活中被广泛应用.下列实例所应用的最主要的几何知识为:
12. 如图,数学知识在生产和生活中被广泛应用.下列实例所应用的最主要的几何知识为:①射击时,瞄准星的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”;
②车轮做成圆形,应用了“圆上各点到圆心的距离相等”;
③学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”;
④地板砖可以做成矩形,应用了“矩形对边相等”.
上述说法正确的是 . (填序号)
 13. 如图,⊙O 中,点 A、O、D 以及点 B、O、C 分别在一条直线上,图中弦的条数有条.
13. 如图,⊙O 中,点 A、O、D 以及点 B、O、C 分别在一条直线上,图中弦的条数有条.
三、解答题
-
14. 已知:如图,、、是的三条半径, , 、分别为、的中点.求证: .
 15. 已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.求证: .
15. 已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.求证: .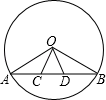
四、综合题
-
16. 已知:如图,在△ABC中, , 以腰AB为直径作 , 分别交BC,AC于点D,E,连接OD,DE.
 (1)、求证:.(2)、若 , 求的度数.17. 公元前5世纪,古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱,在狱中他对方铁窗和圆月亮产生了兴趣.他不断变换观察的位置,一会儿看见圆比正方形大,一会儿看见正方形比圆大,于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了:作一个正方形,使它的面积等于已知圆的面积(1)、设有一个半径为 的圆,则这个圆的周长为 , 面积为 , 作化圆为方得到的正方形的边长为(计算结果保留π)(2)、由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图),包括化圆为方在内的几何三大问题都已被证明是不可能的.但若不受标尺的限制,化圆为方并非难事。达·芬奇(1452--1519)提出用已知圆为底,圆半径的 为高的圆柱,在平面上滚动一周,所得的长方形,其面积恰为圆的面积,然后再将长方形化为等面积的正方形即可设已知圆半径为R,请证明达·芬奇的作法可以完成化圆为方
(1)、求证:.(2)、若 , 求的度数.17. 公元前5世纪,古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱,在狱中他对方铁窗和圆月亮产生了兴趣.他不断变换观察的位置,一会儿看见圆比正方形大,一会儿看见正方形比圆大,于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了:作一个正方形,使它的面积等于已知圆的面积(1)、设有一个半径为 的圆,则这个圆的周长为 , 面积为 , 作化圆为方得到的正方形的边长为(计算结果保留π)(2)、由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图),包括化圆为方在内的几何三大问题都已被证明是不可能的.但若不受标尺的限制,化圆为方并非难事。达·芬奇(1452--1519)提出用已知圆为底,圆半径的 为高的圆柱,在平面上滚动一周,所得的长方形,其面积恰为圆的面积,然后再将长方形化为等面积的正方形即可设已知圆半径为R,请证明达·芬奇的作法可以完成化圆为方