2023-2024学年初中数学九年级上册 27.3 反比例函数的应用 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,直线与x轴相交于点A , 与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是 , 则不等式组的解集是( )
 A、 B、 C、 D、2. 已知反比例函数(k为常数)的图象经过点 . 如图,过点B作直线 与函数的图象交于点A,与x轴交于点C,且 , 过点A作直线 , 交x轴于点F,则线段的长为( )
A、 B、 C、 D、2. 已知反比例函数(k为常数)的图象经过点 . 如图,过点B作直线 与函数的图象交于点A,与x轴交于点C,且 , 过点A作直线 , 交x轴于点F,则线段的长为( ) A、 B、 C、 D、3. 已知一次函数与反比例函数在同一平面直角坐标系中的图象如图所示,则当时,的取值范围是( )
A、 B、 C、 D、3. 已知一次函数与反比例函数在同一平面直角坐标系中的图象如图所示,则当时,的取值范围是( ) A、或 B、或 C、 D、4. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( )
A、或 B、或 C、 D、4. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( ) A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<125. 如图,某加油站计划在地下修建一个容积为的圆柱形石油储存室,则储存室的底面积S(单位:)与其深度h(单位:m)的函数图象大致是( )
A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<125. 如图,某加油站计划在地下修建一个容积为的圆柱形石油储存室,则储存室的底面积S(单位:)与其深度h(单位:m)的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,在平面直角坐标系中,直线与直线分别与函数的图象交点、两点,连结、 , 若的面积为 , 则的值为( ).
6. 如图,在平面直角坐标系中,直线与直线分别与函数的图象交点、两点,连结、 , 若的面积为 , 则的值为( ). A、-2 B、-3 C、-4 D、-67. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( )
A、-2 B、-3 C、-4 D、-67. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( ) A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m28. 如图,过原点的直线与反比例函数 的图象交于 、 两点,点 在第一象限,点 在 轴正半轴上,连接 交反比例函数图象于点 , 为 的平分线,过点 作 的垂线,垂足为 ,连接 ,若 , 的面积为8,则 的值为( )
A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m28. 如图,过原点的直线与反比例函数 的图象交于 、 两点,点 在第一象限,点 在 轴正半轴上,连接 交反比例函数图象于点 , 为 的平分线,过点 作 的垂线,垂足为 ,连接 ,若 , 的面积为8,则 的值为( ) A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10二、填空题
-
9. 如图,正比例函数 , 一次函数和反比例函数的图象在同一直角坐标系中,若 , 则自变量的取值范围是.
 10. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时.
10. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时. 11. 如图,在平面直角坐标系中,的边平行于轴,反比例函数的图象经过的中点和点.若的面积为9,则.
11. 如图,在平面直角坐标系中,的边平行于轴,反比例函数的图象经过的中点和点.若的面积为9,则. 12. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
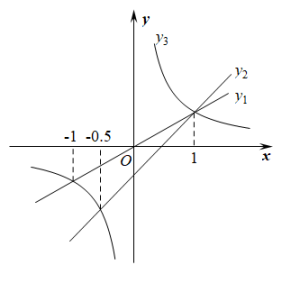
12. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为. 13. 函数y1=x(x≥0),y2=(x>0)的图象如图所示,则以下4个结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③直线x=1与y1 , y2依次交于C,B两点,则BC=3;④当x逐渐增大时,y1随着x的增大而增大y2随着x的增大而减小.其中正确结论的序号是 .
13. 函数y1=x(x≥0),y2=(x>0)的图象如图所示,则以下4个结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③直线x=1与y1 , y2依次交于C,B两点,则BC=3;④当x逐渐增大时,y1随着x的增大而增大y2随着x的增大而减小.其中正确结论的序号是 .
三、解答题
-
14. 如图,一次函数y=x+1的图像与反比例函数y的图像相交,其中一个交点的横坐标是2.求反比例函数的解析式.
 15. 已知近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,求小慧所戴眼镜的度数降低了多少度.
15. 已知近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,求小慧所戴眼镜的度数降低了多少度.四、综合题
-
16. 如图,一次函数y=kx+b与反比例函数y=m/x的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,已知A点的坐标是(2,3),BC=2.
 (1)、求反比例函数与一次函数的关系式;(2)、点P为反比例函数y=m/x图象上的任意一点,若S_POC=3S_ABC,求点P的坐标.17. 如图,点和点是反比例函数图象上的两点,一次函数的图象经过点 , 与轴交于点 , 过点作轴,垂足为 , 连接.已知与的面积满足.
(1)、求反比例函数与一次函数的关系式;(2)、点P为反比例函数y=m/x图象上的任意一点,若S_POC=3S_ABC,求点P的坐标.17. 如图,点和点是反比例函数图象上的两点,一次函数的图象经过点 , 与轴交于点 , 过点作轴,垂足为 , 连接.已知与的面积满足.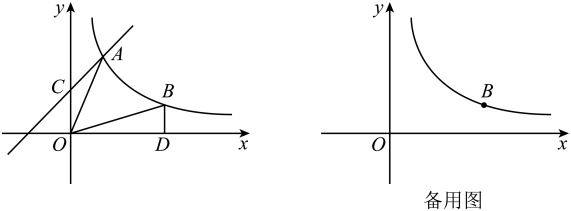 (1)、求的面积和的值;(2)、求直线的表达式;(3)、过点的直线分别交轴和轴于两点, , 若点为的平分线上一点,且满足 , 请求出点的坐标.
(1)、求的面积和的值;(2)、求直线的表达式;(3)、过点的直线分别交轴和轴于两点, , 若点为的平分线上一点,且满足 , 请求出点的坐标.