2023-2024学年初中数学九年级上册 27.2 反比例函数的图像与性质 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 一次函数与反比例函数(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( )
2. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( ) A、 B、 C、 D、3. 已知点 , , 在反比例函数的图象上, , 则下列结论一定成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 如图,已知正方形的面积为9.它的两个顶点 , 是反比例函数( , )的图象上两点,若点的坐标是 , 则的值为( )
A、 B、 C、 D、3. 已知点 , , 在反比例函数的图象上, , 则下列结论一定成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 如图,已知正方形的面积为9.它的两个顶点 , 是反比例函数( , )的图象上两点,若点的坐标是 , 则的值为( )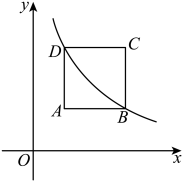 A、3 B、 C、 D、6. 已知点 , , 都在反比例函数的图象上,则下列关系式一定正确的是( )A、 B、 C、 D、7. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、3 B、 C、 D、6. 已知点 , , 都在反比例函数的图象上,则下列关系式一定正确的是( )A、 B、 C、 D、7. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、48. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、1 B、 C、2 D、48. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )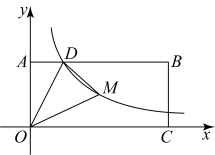 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. 若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数的图象上,则y1 , y2 , y3的大小关系是(用“<”连接).10. 已知一次函数和反比例函数的图象同时经过点 , 则的值是 .11. 如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为;②当平分时,正方形的面积为 .
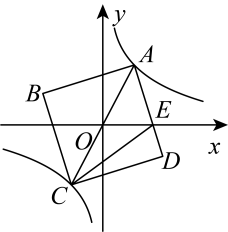 12. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .
12. 如图,菱形的边在x轴的正半轴上,反比例函数的图象经过菱形对角线的中点D和顶点C,若菱形的面积为 , 则点C的坐标为 .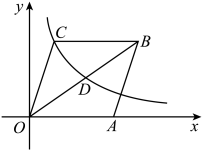 13. 如图,矩形的边平行于轴,反比例函数的图象经过点 , 对角线的延长线经过原点 , 且 , 若矩形的面积是8,则的值为 .
13. 如图,矩形的边平行于轴,反比例函数的图象经过点 , 对角线的延长线经过原点 , 且 , 若矩形的面积是8,则的值为 .
三、解答题
-
14. 已知点p(m,n)是反比例函数图象上一动点,且m≠n,将代数式化简并求值.15. 已知 , 其中与成反比例,与成正比,且当时;当时, , 求关于的函数解析式.
四、综合题
-
16. 如图1,在平面直角坐标系中,反比例函数y=(k>0,k为常数,x>0)的图象经过正方形ABCO的顶点B,点A的坐标是(0,1).点D在线段OA上,点E在射线OC上,以BD,DE为边的平行四边形BDEF的顶点F恰好在该反比例函数的图象上
 (1)、求k的值:(2)、若点D的坐标是(0,),求点E的坐标:(3)、如图2,当点E在OC的延长线上时,连结BE若BD⊥BE,BD=BE.求点D的坐标.17. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .
(1)、求k的值:(2)、若点D的坐标是(0,),求点E的坐标:(3)、如图2,当点E在OC的延长线上时,连结BE若BD⊥BE,BD=BE.求点D的坐标.17. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .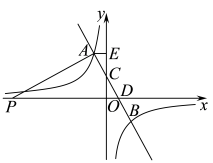 (1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.
(1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.