2023-2024学年初中数学九年级上册 26.4 解直角三角形的应用同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 图中的梯形ABCD是水坝的一个截面图，阴影部分是外坡面土方的部分．其中 $A D ∥ B C$ ， $∠ C = 9 0^{o}$ ， $∠ B = 45^{o}$ ， $∠ D E C = 60^{o}$ ， $A B = 10 \sqrt{6}$ m，AD＝5m，则坝底外坡面土方的水平宽度BE长为（）

A、 $10 \sqrt{3}$ m B、 $(10 \sqrt{3} - 5)$ m C、 $(10 \sqrt{3} + 5)$ m D、 $(5 \sqrt{3} + 5)$ m

查看试题解析
2. 某驱逐舰在海上执行任务后刚返回到港口A，接到上级指令，发现在其北偏东 $30 °$ 方向上有一艘可疑船只C，与此同时在港口A处北偏东 $60 °$ 方向上且距离 $10 k m$ 处有另一艘驱逐舰B也收到了相关指令，驱逐舰B恰好在可疑船只C的南偏东 $30 °$ 的方向上，则可疑船只C距离港口A的距离为（　　）

A、 $\frac{5 \sqrt{3}}{3} k m$ B、 $\frac{10 \sqrt{3}}{3} k m$ C、 $\frac{20 \sqrt{3}}{3} k m$ D、 $10 \sqrt{3} k m$

查看试题解析
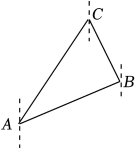3. 如图，某商场一楼与二楼之间的电梯示意图.∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（）

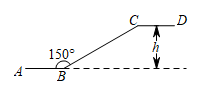A、 $\frac{8}{3} \sqrt{3}$ m B、 $4 \sqrt{3}$ m C、8m D、4m

查看试题解析
4. 数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为37米，当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为 $30 °$ ，则旗杆的高度约为（）

A、 $15 \sqrt{3}$ 米 B、 $(37 - 15 \sqrt{3}) 米$ C、 $(45 - 15 \sqrt{3}) 米$ D、22.5米

查看试题解析
5. 如图，某校教学楼 $A B$ 与 $C D$ 的水平间距 $B D = a m$ ，在教学楼 $C D$ 的顶部 $C$ 点测得教学楼 $A B$ 的顶部 $A$ 点的仰角为 $α$ ，测得教学楼 $A B$ 的底部 $B$ 点的俯角为 $β$ ，则教学楼 $A B$ 的高度是（）

A、 $(a t a n α + a t a n β) m$ B、 $(\frac{a}{t a n α} + \frac{a}{t a n β}) m$ C、 $(a s i n α + a s i n β) m$ D、 $(a c o s α + a c o s β) m$

查看试题解析
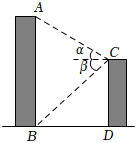6. $2022$ 年 $4$ 月 $16$ 日，神舟十三号载人飞船返回舱在东风着陆场成功着陆，神舟十三号载人飞行任务收得圆满成功，中国航天，又站在了一个新的起点.如图 $2021$ 年 $10$ 月 $16$ 日，神舟十三号载人飞船从地面 $О$ 处成功发射，当飞船到达点 $A$ 时，地面 $D$ 处的雷达站测得 $A D = 4000$ 米，仰角为 $30 °$ ， $3$ 秒后，飞船直线上升到达点 $B$ 处，此时地面 $C$ 处的雷达站测得 $B$ 处的仰角为 $45 °$ .点 $O$ ， $C$ ， $D$ 在同一直线上，已知 $C$ ， $D$ 两处相距 $460$ 米，则飞船从 $A$ 到 $B$ 处的平均速度为（）米 $/$ 秒.（结果精确到 $1$ 米；参考数据： $\sqrt{3} \approx 1.732$ ， $\sqrt{2} \approx 1.414$ ）

A、336 B、335 C、334 D、333

查看试题解析
7. 如图，轮船在A处观测灯塔C位于北偏西 $70 °$ 方向上，轮船从A处以每小时40海里的速度沿南偏西 $50 °$ 方向匀速航行，1小时后到达码头B处，此时，观测灯塔C位于北偏西 $25 °$ 方向上，则下列说法正确的是（）

A、 $∠ C B A = 85 °$ B、点B到 $A C$ 的距离为 $20 \sqrt{2}$ 海里 C、 $B C = 20 \sqrt{6}$ 海里 D、点B在点C的南偏东 $65 °$ 的方向上

查看试题解析
8. 如图，在平行四边形OABC中，边OC在x轴上，点A（1， $\sqrt{3}$ ），点C（3，0）．按以下步骤作图：分别以点B，C为圆心，大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于E，F两点；作直线EF，交AB于点H；连接OH，则OH的长为（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、2 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析

二、填空题

9. 2023年岳阳举办以“跃马江湖”为主题的马拉松赛事．如图，某校数学兴趣小组在 $A$ 处用仪器测得赛场一宣传气球顶部 $E$ 处的仰角为 $21.8 °$ ，仪器与气球的水平距离 $B C$ 为20米，且距地面高度 $A B$ 为1.5米，则气球顶部离地面的高度 $E C$ 是米（结果精确到0.1米， $s i n 21.8 ° \approx 0.3714 ， c o s 21.8 ° \approx 0.9285 ， t a n 21.8 ° \approx 0.4000$ ）．

查看试题解析
10. 如图，供给船要给C岛运送物资，从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛．测得海岸线上的港口B在C岛南偏东50°方向．若A，B两港口之间的距离为65nmile，则C岛到港口B的距离是nmile．

查看试题解析
11. 如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成.在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行，

(1)、当∠EFH＝55°，BC∥EF时，∠ABC＝度；

(2)、如图3为了参与另一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF
所在直线互相垂直，且∠EFH＝78°，此时∠ABC＝度．

查看试题解析
12. 如(图1)，某学校楼梯墙面上悬挂了四幅全等的正方形画框，画框下边缘与 $B$ 水平地面平行．如(图2)，画框的左上角顶点 $B$ ， $E$ ， $F$ ， $G$ 都在直线 $A B$ 上，且 $B E = E F = F G$ ，楼梯装饰线条所在直线 $C D / / A B$ ，延长画框的边 $B H$ ， $M N$ 得到平行四边形ABCD．若直线 $P Q$ 恰好经过点 $D$ ， $A B = 275 c m$ ， $C H = 100 c m$ ， $∠ A = 60 °$ ，则正方形画框的边长为

查看试题解析
13. 衢州儿童公园有摩天轮，水上乐园等娱乐设施，其中的摩天轮半径为20米，水上乐园的最高处到地面的距离为32米；如图，当摩天轮的座舱A旋转至与水上乐园最高处高度相同时，地面某观测点P与座舱A，摩天轮圆心O恰好在同一条直线上，此时测得 $∠ A P C = 30 °$ ，则 $P C$ 的距离为米；此时另一座舱B位于摩天轮最低点，摩天轮旋转一周要12分钟，若摩天轮继续逆时针旋转一周，当从座舱A观测座舱B的俯角为45°时，经过了分钟.

查看试题解析

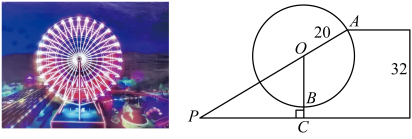
三、解答题

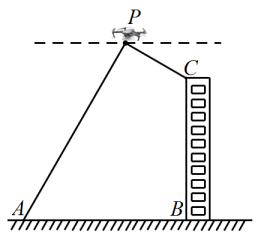
14. 无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度 $B C$ ，无人机在空中点P处，测得点P距地面上A点80米，点A处俯角为 $60 °$ ，楼顶C点处的俯角为 $30 °$ ，已知点A与大楼的距离 $A B$ 为70米（点A，B，C，P在同一平面内），求大楼的高度 $B C$ （结果保留根号）

查看试题解析
15. 如图，某数学兴趣小组为了测量古树 $D E$ 的高度，采用了如下的方法：先从与古树底端 $D$ 在同一水平线上的点A出发，沿斜面坡度为 $i = 2 ： \sqrt{3}$ 的斜坡 $A B$ 前进 $20 \sqrt{7} m$ 到达点 $B$ ，再沿水平方向继续前进一段距离后到达点 $C$ ．在点 $C$ 处测得古树 $D E$ 的顶端 $E$ 的俯角为 $37 °$ ，底部 $D$ 的俯角为 $60 °$ ，求古树 $D E$ 的高度（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $c o s 37 ° \approx \frac{4}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ，计算结果用根号表示，不取近似值）．

查看试题解析

四、综合题

16. 如图，光从空气斜射入水中，入射光线 $A B$ 射到水池的水面 $B$ 点后折射光线 $B D$ 射到池底点 $D$ 处，入射角 $∠ A B M = 30 °$ ，折射角 $∠ D B N = 22 °$ ；入射光线 $A C$ 射到水池的水面 $C$ 点后折射光线 $C E$ 射到池底点 $E$ 处，入射角 $∠ A C M' = 60 °$ ，折射角 $∠ E C N' = 40.5 ° . D E / / B C$ ， $M N$ 、 $M' N'$ 为法线 $.$ 入射光线 $A B$ 、 $A C$ 和折射光线 $B D$ 、 $C E$ 及法线 $M N$ 、 $M' N'$ 都在同一平面内，点 $A$ 到直线 $B C$ 的距离为 $6$ 米．

(1)、求 $B C$ 的长； $($ 结果保留根号 $)$

(2)、如果 $D E = 8.72$ 米，求水池的深 $. ($ 参考数据： $\sqrt{2}$ 取 $1.41$ ， $\sqrt{3}$ 取 $1.73$ ， $s i n 22 °$ 取 $0.37$ ， $c o s 22 °$ 取 $0.93$ ， $t a n 22 °$ 取 $0.4$ ， $s i n 40.5 °$ 取 $0.65$ ， $c o s 40.5 °$ 取 $0.76$ ， $t a n 40.5 °$ 取 $0.85)$

查看试题解析
17. 随着科技的发展，无人机已广泛应用于生产生活，如代替人们在高空测量距离和高度．圆圆要测量教学楼 $A B$ 的高度，借助无人机设计了如下测量方案：如图，圆圆在离教学楼底部 $24 \sqrt{3}$ 米的C处，遥控无人机旋停在点C的正上方的点D处，测得教学楼 $A B$ 的顶部B处的俯角为 $30 °$ ， $C D$ 长为 $49.6$ 米．已知目高 $C E$ 为 $1.6$ 米．

(1)、求教学楼 $A B$ 的高度．

(2)、若无人机保持现有高度沿平行于 $C A$ 的方向，以 $4 \sqrt{3}$ 米/秒的速度继续向前匀速飞行，求经过多少秒时，无人机刚好离开圆圆的视线 $E B$ ．

查看试题解析
18. 图1是某简易座椅，图2是其侧面示意图，固定点O为椅腿 $A B$ 和 $C D$ 的中点，靠背 $E F$ 的一端固定在 $A O$ 上的点E处，将 $E F$ 绕点E顺时针旋转180°后与 $E B$ 重合，此时靠背收拢．已知 $A B = C D = 40 c m$ ， $A E = 10 c m$ ， $∠ A O C = 74 °$ ．

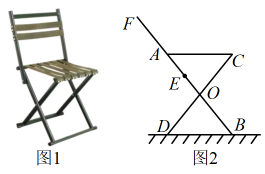(1)、求坐垫 $A C$ 的长．

(2)、在收拢靠背的过程中，求点F到点C距离的最小值．（结果精确到 $1 c m$ ；参考数据： $s i n 37 ° = c o s 53 ° \approx 0.6$ ， $s i n 53 ° = c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ ， $t a n 53 ° \approx 1.33$ ， $\sqrt{97} \approx 9.85$ ）

查看试题解析

2023-2024学年初中数学九年级上册 26.4 解直角三角形的应用 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 26.4 解直角三角形的应用同步分层训练培优卷(冀教版)