2023-2024学年初中数学九年级上册 26.3 解直角三角形同步分层训练基础卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $c o s A = \frac{1}{3}$ ，则 $t a n B$ 的值为（）

A、2 B、3 C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{\sqrt{2}}{4}$

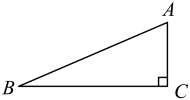查看试题解析
2. 在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（）

A、tanB= $\frac{3}{4}$ B、sinB= $\frac{4}{3}$ C、sinB= $\frac{4}{5}$ D、cosB= $\frac{4}{5}$

查看试题解析
3. 如图，已知Rt $△ A B C ， C D$ 是斜边 $A B$ 边上的高，那么下列结论正确的是（）

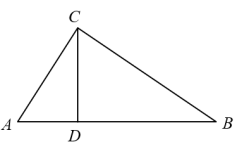A、 $C D = A B \cdot t a n B$ B、 $C D = A D \cdot c o t A$ C、 $C D = A C \cdot s i n B$ D、 $C D = B C \cdot c o s A$

查看试题解析
4. 如图，窗子高AB=m米，窗子外面上方0.2米的点C处安装水平遮阳板CD=1米，当太阳光线与水平线成α=60°角时，光线刚好不能直接射入室内，则m的值是（）

A、m= $\sqrt{3}$ +0.8 B、m= $\sqrt{3}$ +0.2 C、m= $\sqrt{3}$ -0.2 D、m= $\sqrt{3}$ -0.8

查看试题解析
5. 如图，在Rt△ABC中，若 $t a n A = \frac{1}{2}$ ， AB＝10，则△ABC的面积为（）

A、20 B、15 C、 $3 \sqrt{5}$ D、 $4 \sqrt{5}$

查看试题解析
6. 如图， $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 29 °$ ， $B C = 8$ ，则 $A B$ 为（）

A、 $\frac{8}{\sin 29 °}$ B、 $8 \sin 29 °$ C、 $\frac{8}{\tan 29 °}$ D、 $8 \tan 29 °$

查看试题解析
7. 如图所示，菱形 $A B C D$ 的周长为 $20 c m$ ， $D E ⊥ A B$ ，垂足为E， $s i n A = \frac{3}{5}$ ，则下列结论正确的个数有（）
① $D E = 3 c m$ ， ② $B E = 1 c m$ ， ③菱形的面积为 $15 c m^{2}$ ， ④ $B D = 2 \sqrt{10} c m$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，一把梯子 $A B$ 靠在垂直水平地面的墙上，梯子底端A到墙面的距离 $A C$ 为6米，若梯子与地面的夹角为α，则梯子 $A B$ 的长为（）

A、 $6 s i n α$ 米 B、 $6 c o s α$ 米 C、 $\frac{6}{s i n α}$ 米 D、 $\frac{6}{c o s α}$ 米

查看试题解析

二、填空题

9. 如图，测得某医院的自动扶梯的长为m，自动扶梯与地面所成的角为α，则该自动扶梯到达的高度n为.

查看试题解析
10. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{1}{3}$ ， $B C = 2$ ，则 $A C =$ ．

查看试题解析
11. 如图， $A B = A C = 4$ ， $∠ B A C = 90 °$ ，点 $M$ 是线段 $A C$ 上一个动点，连接 $B M$ ，将线段 $B A$ 沿直线 $B M$ 进行翻折，点 $A$ 落在点 $N$ 处，连接 $C N$ ，以 $C N$ 为斜边在直线 $C N$ 的左侧 $($ 或者下方 $)$ 构造等腰直角三角形 $C N D$ ，则点 $M$ 从 $A$ 运动到 $C$ 的过程中，线段 $C D$ 的最小值是，当 $M$ 从点 $A$ 运动到点 $C$ 时，点 $D$ 的运动总路径长是．

查看试题解析
12. 如图，OC平分∠AOB，P是边OA上一点，以点P为圆心、大于点P到OB的距离为半径作弧，交OB于点E、F，再分别以点E、F为圆心，大于 $\frac{1}{2}$ EF的长为半径作弧，两弧交于点D．作直线PD分别交OC、OB于点G、Q．若sin∠AOB＝ $\frac{\sqrt{3}}{2}$ ， OP＝4 $\sqrt{3}$ ，则△OPG的面积为．

查看试题解析
13. 如图，点F，G分别在正方形ABCD的边BC，CD上，E为AB中点，连结ED，正方形FGQP的边PQ恰好在DE上，记正方形ABCD面积为 $S_{1}$ ，正方形FPQG面积为 $S_{2}$ ，则 $S_{1} ： S_{2}$ 的值为．

查看试题解析

三、解答题

14. $Δ A B C$ 中， $∠ B = 45 °$ ， $∠ B A C = 15 °$ ， $A C = 10 c m$ ，求 $B C$ 边的长度．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 9 0^{∘}$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 边于点D， $D E ⊥ A B$ 于点E，若 $B D = 5$ ， $c o s B = \frac{4}{5}$ ，求 $A C$ 的长．

查看试题解析

四、综合题

16. 如图， $A D$ 是 $△ A B C$ 的高，若 $A D = 6$ ， $t a n C = \frac{3}{2}$ ， $B C = 12$ ．

(1)、求 $C D$ 边的长；

(2)、求 $c o s B$ 的值．

查看试题解析
17. 如图，在矩形ABCD中，点E为边AB上的一动点（点E不与点A，B重合），连接DE，过点C作CF⊥DE，垂足为F．

(1)、求证：△ADE∽△FCD；

(2)、若AD＝6，tan∠DCF＝ $\frac{1}{3}$ ，求AE的长．

查看试题解析

2023-2024学年初中数学九年级上册 26.3 解直角三角形 同步分层训练基础卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 26.3 解直角三角形同步分层训练基础卷(冀教版)