2023-2024学年初中数学九年级上册 26.2 锐角三角函数的计算同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 已知 $∠ A$ 为锐角， $c o s A = \frac{1}{2}$ ，则 $∠ A$ 的大小是（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
2. 在 $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ，则下列式子定成立的是 $($ $)$

A、 $s i n A = s i n B$ B、 $c o s A = c o s B$ C、 $t a n A = t a n B$ D、 $s i n A = c o s B$

查看试题解析
3. 2022年2月4日在北京举办了第24届冬季奥运会，很多学校都开展冰雪项目学习，如图，一位同学乘滑雪板沿斜坡笔直滑下100米，若斜坡的坡比为 $t a n 38 ° ： 1$ ，用计算器求下滑的水平距离，则下列按键顺序正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28km/时的速度向正东航行，半小时到B处，在B处看见灯塔M在北偏东15°方向，此时，灯塔M与渔船的距离是（）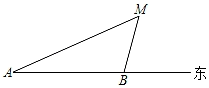

A、7 $\sqrt{2}$ km B、14 $\sqrt{2}$ km C、7km D、14km

查看试题解析
5. 如图， $E F$ 与 $A B$ ， $B C$ ， $C D$ 分别交于点E，G，F，且 $∠ 1 = ∠ 2 = 30 °$ ， $E F ⊥ A B$ ，则下列结论错误的是（）

A、 $A B / / C D$ B、 $∠ 3 = 60 °$ C、 $F G = \frac{1}{2} F C$ D、 $G F ⊥ C D$

查看试题解析
6. 如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为（）

A、2acos32°米 B、2atan32°米 C、 $\frac{2 a}{s i n 32 °}$ 米 D、 $\frac{2 a}{t a n 32 °}$ 米

查看试题解析
7. 如图，在平行四边形OABC中，边OC在x轴上，点A（1， $\sqrt{3}$ ），点C（3，0）．按以下步骤作图：分别以点B，C为圆心，大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于E，F两点；作直线EF，交AB于点H；连接OH，则OH的长为（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、2 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
8. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $P$ 为 $A C$ 上一动点，若 $B C = 4$ ， $A C = 6$ ，则 $\sqrt{2} B P + A P$ 的最小值为（）

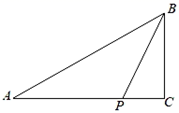A、5 B、10 C、 $5 \sqrt{2}$ D、 $10 \sqrt{2}$

查看试题解析

二、填空题

9. 阅读材料：余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理，运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题．余弦定理是这样描述的：在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍．
用公式可描述为：a²＝b²＋c²﹣2bccosA

b²＝a²＋c²﹣2accosB

c²＝a²＋b²﹣2abcosC

现已知在△ABC中，AB＝3，AC＝4，∠A＝60°，则BC＝．

查看试题解析
10. △ABC中，AD是BC边上的高，AD＝4， $A C = 4 \sqrt{2}$ ， AB＝8，则 $∠ B A C =$ ．

查看试题解析
11. 如图，在矩形 $A B C D$ 中，点 $E$ 为矩形内一点，且 $A B = 1$ ， $A D = \sqrt{3} ， ∠ B A E = 75 ° ， ∠ B C E = 60 °$ ，则四边形 $A B C E$ 的面积是．

查看试题解析
12. 如图，在正方形 $A B C D$ 中，点E、F分别在边 $A D 、 A B$ 上， $E F ⊥ C E$ ．将 $△ C D E$ 沿直线CE翻折，如果点D的对应点恰好落在线段 $C F$ 上，那么 $∠ E F C$ 的正切值是．

查看试题解析
13. 如图，点A在线段BD上，在BD的同侧作等腰直角 $△ A B C$ 和等腰直角 $△ A D E$ ，CD与BE、AE分别交于点P，M.对于下列结论：① $△ B A E ∽ △ C A D$ ；② $M P . M D = M A \cdot M E$ ；③ $2 C B^{2} = C P \cdot C M$ ；④ $\sin ∠ C P B = \frac{\sqrt{3}}{2}$ ；其中正确的结论有.（写出所有正确结论的序号）

查看试题解析

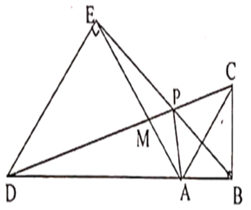
三、解答题

14. 先化简，再求代数式 $(1 + \frac{1}{x + 1}) \div \frac{x^{2} + 4 x + 4}{x + 1}$ 的值，其中 $x = 6 c o s 45 ° - 2 t a n 45 °$ ．

查看试题解析

四、综合题

15. 如图，在菱形ABCD中，对角线AC，BD相交于点 $O$ ，点P，Q分别是边BC，线段OD上的点，连接AP，QP，AP与OB相交于点 $E$ .

(1)、如图1，连接QA.当 $Q A = Q P$ 时，试判断点 $Q$ 是否在线段PC的垂直平分线上，并说明理由；

(2)、如图2， $∠ A P B = 9 0^{°}$ ，且 $∠ B A P = ∠ A D B$ ，
①求证： $A E = 2 E P$ ；

②当 $O Q = O E$ 时，设 $E P = a$ ，求PQ的长（用含a的代数式表示）.

查看试题解析
16. 如图，平行四边形 $A B C D$ 中， $A E 、 C F$ 分别是 $∠ B A D 、 ∠ B C D$ 的平分线，且 $E 、 F$ 分别在边 $B C 、 A D$ 上， $A E = A F$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $∠ A B C = 60 °$ ， $△ A B E$ 的面积等于 $4 \sqrt{3}$ ，求平行线 $A B$ 与 $D C$ 间的距离．

查看试题解析

2023-2024学年初中数学九年级上册 26.2 锐角三角函数的计算 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 26.2 锐角三角函数的计算同步分层训练培优卷(冀教版)