2023-2024学年初中数学九年级上册 26.1 锐角三角函数 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 在平面直角坐标系中的位置如图所示, , , 则点B的坐标为( )
 A、 B、 C、 D、2. 如图,由边长为1的小正方形组成的网格中,的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( )
A、 B、 C、 D、2. 如图,由边长为1的小正方形组成的网格中,的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( )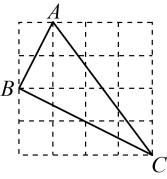 A、 B、 C、 D、3. 如图,圆规两脚 , 张开的角度 , , 则两脚张开的距离为( )
A、 B、 C、 D、3. 如图,圆规两脚 , 张开的角度 , , 则两脚张开的距离为( ) A、 B、 C、 D、4. 如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 小正方形的对角线向两边延长,分别交边于点 , 交边于点 . 若是的中点,则的值为( )
A、 B、 C、 D、4. 如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 小正方形的对角线向两边延长,分别交边于点 , 交边于点 . 若是的中点,则的值为( )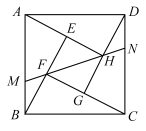 A、 B、 C、 D、5. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,测得 , , , 则点到的距离为( )
A、 B、 C、 D、5. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,测得 , , , 则点到的距离为( ) A、 B、 C、 D、6. 如图,菱形的边长为2, , 则菱形的面积是( )
A、 B、 C、 D、6. 如图,菱形的边长为2, , 则菱形的面积是( ) A、 B、 C、 D、7. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
A、 B、 C、 D、7. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
① ② ③当时,
A、0个 B、1个 C、2个 D、3个8. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )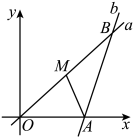 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
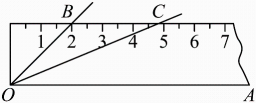
9. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .
 10. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .
10. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .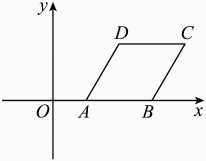 11. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形如果图中与的面积比为 , 那么的值为 .
11. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形如果图中与的面积比为 , 那么的值为 . 12. 如图,在矩形ABCD中,AB=3,AD=4,点E是AD的中点,点P是BE上的动点,点Q是PC的中点,连接AQ , 则AQ长的最小值为 .
12. 如图,在矩形ABCD中,AB=3,AD=4,点E是AD的中点,点P是BE上的动点,点Q是PC的中点,连接AQ , 则AQ长的最小值为 . 13. 如图,在中, , 点是边上的一动点.已知 , 现将绕点按逆时针方向旋转,点是边的中点,则 , 长度的最小值为 .
13. 如图,在中, , 点是边上的一动点.已知 , 现将绕点按逆时针方向旋转,点是边的中点,则 , 长度的最小值为 .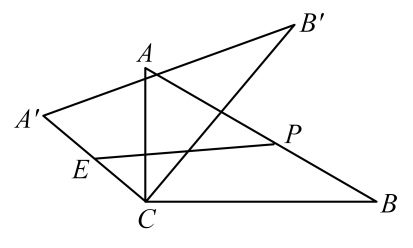
三、作图题
-
14. 图①,图②,图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上,在图①,图②,图③给定的网格中按要求画图.(保留作图痕迹)
 (1)、在图①中,在线段上画出点 , 使 .(2)、在图②中,画出一个格点 , 使是以为斜边的等腰直角三角形.(3)、在图③中,在线段上画出点 , 使 .
(1)、在图①中,在线段上画出点 , 使 .(2)、在图②中,画出一个格点 , 使是以为斜边的等腰直角三角形.(3)、在图③中,在线段上画出点 , 使 .四、综合题
-
15. 数学活动课上,老师组织数学小组的同学进行以“三角形卡片拼接与变换”为主题的数学学习活动.他们准备若干个 , 的特殊直角三角形卡片,其中在三角形卡片中, , , .
 (1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .
(1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .①求证:四边形是平行四边形;
②连接交于点 , 求的面积;
(2)、在(1)的条件下,将一条直角边与重合的等腰直角三角形卡片与四边形拼成如图2所示的平面图形,请求出点到的距离;(3)、一个斜边长度与相等的三角板( , )如图3摆放,将绕点A顺时针旋转,旋转角为 , 旋转后的三角形记为 . 在旋转过程中,直线所在的直线与直线 , 交于 , 两点,当为等腰三角形时,请直接写出的长.16. 在中, , 点E在上,点G在上,点F在的延长线上,连接 . , . (1)、如图1,当时,请用等式表示线段与线段的数量关系;(2)、如图2,当时,写出线段和之间的数量关系,并说明理由;(3)、在(2)的条件下,当点G是的中点时,连接 , 求的值.17. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题:
(1)、如图1,当时,请用等式表示线段与线段的数量关系;(2)、如图2,当时,写出线段和之间的数量关系,并说明理由;(3)、在(2)的条件下,当点G是的中点时,连接 , 求的值.17. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题: (1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
(1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
-