2023-2024学年初中数学九年级上册 25.7 相似多边形和图形的位似 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,小明在边长均为1的正方形网格中,分别作了和 , 其中三个顶点坐标分别为 , , , 若和是以原点为位似中心的位似图形,则( )
 A、 B、 C、 D、2. 在平面直角坐标系中,已知点 , 以原点O为位似中心,相似比为 , 把缩小,则点A的对应点的坐标是( )A、 B、 C、或 D、或3. 如图,与位似,位似中心为点.若的周长与的周长比为 , 则的值为( )
A、 B、 C、 D、2. 在平面直角坐标系中,已知点 , 以原点O为位似中心,相似比为 , 把缩小,则点A的对应点的坐标是( )A、 B、 C、或 D、或3. 如图,与位似,位似中心为点.若的周长与的周长比为 , 则的值为( ) A、 B、 C、 D、4. 如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到 , 则的长为( )
A、 B、 C、 D、4. 如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到 , 则的长为( ) A、 B、 C、或 D、或5. 每年秋季开学,学校组织同学们进行视力测试,如图是视力表的一部分,其中开口向上的两个“”之间的变换是( )
A、 B、 C、或 D、或5. 每年秋季开学,学校组织同学们进行视力测试,如图是视力表的一部分,其中开口向上的两个“”之间的变换是( ) A、平移 B、对称 C、位似 D、旋转6. 将一张()纸片,以它的一边为边长剪去一个菱形,将余下的平行四边形中,再以它的一边为边长剪去一个菱形,若剪去两个菱形后所剩下的平行四边形与原来相似,则的相邻两边与的比值是( )A、 B、 C、或 D、或或7. 如图,E,F,G,H分别是矩形四条边上的点,连接相交于点I,且 , , 矩形矩形 , 连接交于点P,Q,下列一定能求出面积的条件是( )
A、平移 B、对称 C、位似 D、旋转6. 将一张()纸片,以它的一边为边长剪去一个菱形,将余下的平行四边形中,再以它的一边为边长剪去一个菱形,若剪去两个菱形后所剩下的平行四边形与原来相似,则的相邻两边与的比值是( )A、 B、 C、或 D、或或7. 如图,E,F,G,H分别是矩形四条边上的点,连接相交于点I,且 , , 矩形矩形 , 连接交于点P,Q,下列一定能求出面积的条件是( )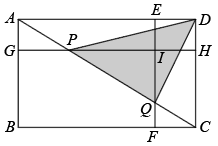 A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差8. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差8. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )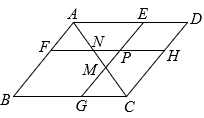 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是.
 10. 一个六边形六边长分别为 , , , , , , 另一个与它相似的六边形的最短边为 , 则其周长为 .11. 如图,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1∶2,∠OCD=90°,CO=CD=2,则点B的坐标为 .
10. 一个六边形六边长分别为 , , , , , , 另一个与它相似的六边形的最短边为 , 则其周长为 .11. 如图,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1∶2,∠OCD=90°,CO=CD=2,则点B的坐标为 . 12. 如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形 ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形 ABCD相似,则 AB:BC 的值为.
12. 如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形 ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形 ABCD相似,则 AB:BC 的值为. 13. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .
13. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .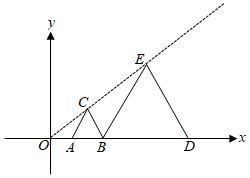
三、解答题
-
14. 如图,△ABC的三个顶点的坐标分别为A(3,1),B(1,2),C(4,3).以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍得到△A1B1C1 , 作出△A1B1C1 , 并写出A1 , B1 , C1的坐标;
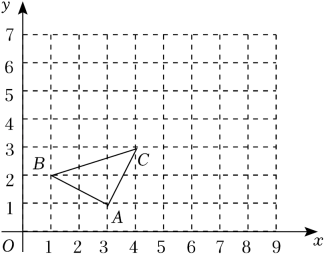 15. 放缩尺是一种绘图工具,它能把图形放大或缩小.
15. 放缩尺是一种绘图工具,它能把图形放大或缩小.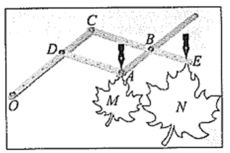
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, , , 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 , , 可证得以下结论:
①和为等腰三角形,则 , (180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
四、综合题
-
16. 学完“探索三角形相似的条件”之后,小明所在的学习小组尝试探索四边形相似的条件,以下是他们的思考,请你和他们一起完成探究过程.
(定义)四边成比例,且四角分别相等的两个四边形叫做相似四边形.
(1)、(初步思考)小明根据探索三角形相似的条件所获得的经验,考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”,“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件,于是,可以从“四边成比例,且一角对应相等的两个四边形相似”,“三边成比例,且两角分别相等的两个四边形相似”,“两边成比例,且三角分别相等的两个四边形相似”来探究.
(2)、(深入探究)学习小组一致认为,“四边成比例,且一角对应相等的两个四边形相似”是真命题,请结合图形完成证明.
已知:四边形 和四边形 中, , .
求证:四边形 四边形 .证明:
 (3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:
(3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:①“三边成比例,两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”;
②“三边成比例,两邻角分别相等且都不是其中两边的夹角的两个四边形相似”;
③“三边成比例及其两夹角分别相等的两个四边形相似”;
④“三边成比例,两对角分别相等的两个四边形相似”.
其中真命题是.(填写所有真命题的序号)
(4)、请你完成“两边成比例,且三角分别相等的两个四边形相似”的探究过程.