2023-2024学年初中数学九年级上册 25.6 相似三角形的应用 同步分层训练基础卷(冀教版)
试卷更新日期：2023-08-12 类型：同步测试
一、选择题
-
1. 如图，它是物理学中小孔成像的原理示意图，已知物体 ， 根据图中尺寸 ， 则的长应是（ ）
A、15 B、30 C、20 D、102. 高4米的旗杆在水平地面上的影长为6米，此时测得附近一个建筑物的影长24米，则该建筑物的高度为（ ）A、10米 B、16米 C、26米 D、36米3. 如图，线段AB，EF，CD分别表示人，竹竿，楼房的高度，且A，E，C在同一直线上．测得人和竹竿的水平距离为1.2m，人和楼房的水平距离为20m，人的高度为1.5m，竹竿的高度为3m，则楼房的高度是（ ）
A、25m B、26.5m C、50m D、51.5m4.如图，将一张三角形纸片沿虚线剪成甲、乙、丙三块，其中甲、丙为梯形，乙为三角形．根据图中标示的边长数据，比较甲、乙、丙的面积大小，下列判断正确的是（ ）
A、乙＞丙＞甲 B、丙＞乙＞甲 C、甲＞丙＞乙 D、无法判断5. “跳眼法”是炮兵常用的一种简易测距方法，如图，点A为左眼，点B为右眼，点O为右手大拇指，点C为敌人的位置，点D为敌人正左侧方的某一个参照物 ， 已知大多数人的眼距长约为6.4厘米左右，而手臂长约为64厘米左右．若的估测长度为50米，那么的大致距离为（ ）米．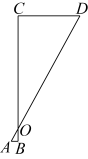
A、250 B、320 C、500 D、7506. 如图，广场上有一盏路灯挂在高的电线杆顶上，记电线杆的底部为 ． 把路灯看成一个点光源，一名身高的女孩站在点处， ， 则女孩的影子长为（ ）
A、 B、 C、 D、7. 如图，有一块三角形土地，它的底边 米，高 米，某单位要沿着底边 修一座底面是矩形 的大楼，矩形的长宽比为5：4，则这座大楼的地基面积是（ ）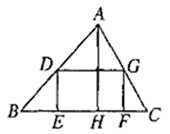
A、 B、 C、 D、8. 如图所示为我市某农村一古老的捣碎器，已知支撑柱AB的高为0.3米，踏脚着地时捣头点E距离地面0.8米 ，则捣头点E着地时，踏脚点D距离地面（ ）
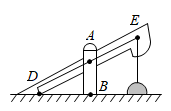A、0.4 米 B、0.48米 C、0.5 米 D、0.8米二、填空题
-
9. 如图是小孔成像原理的示意图， ， ， . 若物体的高度为 ， 则像的高度是.
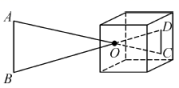10. 如图是用卡钳测量容器内径的示意图，现量得卡钳上 ， 两个端点之间的距离为 ， ，则容器的内径是.
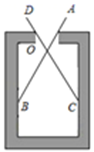11. 如图，某小区车库出入口的栏杆短臂 长1m，长臂 长8m，当短臂外端 下降0.5m时，长臂外端 升高.
12. 如图，中边 ， 高 ， 正方形的四个顶点分别为三边上的点（点 ， 为上的点，点为上的点，点为上的点），则正方形的边长为.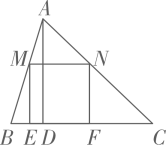
13. 小刚身高180cm，他站立在阳光下的影子长为90cm，他把手臂竖直举起，此时影子长为115cm，那么小刚的手臂超出头顶cm．三、解答题
-
14. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度，他们的测量方案如下：当雯雯站在旗杆正前方地面上的点D处时，笑笑在地面上找到一点G，使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上，并测得DG＝2.8m；然后雯雯向前移动1.5m到达点F处，笑笑同样在地面上找到一点H，使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上，并测得GH＝1.7m，已知图中的所有点均在同一平面内，AB⊥BH，CD⊥BH，EF⊥BH，雯雯的身高CD＝EF＝1.6m.请你根据以上测量数据，求该校旗杆的高度AB.
15. 如图，乐乐测得学校门口栏杆的短臂长1米，长臂长4米，当短臂外端A下降米时，求长臂外端B升高多少米？
四、综合题
-
16. 如图1，长、宽均为3cm，高为8cm的长方体容器，放置在水平桌面上，里面盛有水，水面高为6cm，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，将这个情景转化成几何图形，如图3所示．
(1)、利用图1、图2所示水的体积相等，求的长；(2)、求水面高度 ．17. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD（PM⊥MN）的示意图，设油画AD与墙壁的夹角∠PAD＝α，此时小然的眼睛与油画底部A处于同一水平线上，视线恰好落在油画的中心位置E处，且与AD垂直．已知油画的长度AD为100cm．
(1)、视线∠ABD的度数为 .（用含α的式子表示）(2)、当小然到墙壁PM的距离AB＝250cm时，求油画顶部点D到墙壁PM的距离．