2023-2024学年初中数学九年级上册 25.5 相似三角形的性质 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图是由边长为1的小正方形组成的网格,点A,B都在格点(小正方形的顶点)上,点C为与网格水平线的交点,则的长为( )
 A、 B、 C、 D、2. 如图,是边边上的两点,且 , 若 , 则与的周长之比为( )
A、 B、 C、 D、2. 如图,是边边上的两点,且 , 若 , 则与的周长之比为( ) A、 B、 C、 D、3. 如图,平行四边形的对角线交于点O,E是的中点,连接 . 若的面积是2,则四边形的面积是( )
A、 B、 C、 D、3. 如图,平行四边形的对角线交于点O,E是的中点,连接 . 若的面积是2,则四边形的面积是( ) A、5 B、6 C、7 D、84. 如图,在直角坐标系中,菱形顶点A,B,C在坐标轴上,若点B的坐标为 , , 当恰好第一次落在线段上时,的坐标为( )
A、5 B、6 C、7 D、84. 如图,在直角坐标系中,菱形顶点A,B,C在坐标轴上,若点B的坐标为 , , 当恰好第一次落在线段上时,的坐标为( )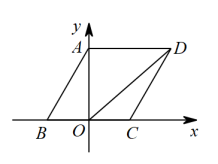 A、 B、 C、 D、5. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )
A、 B、 C、 D、5. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )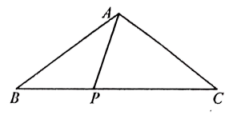 A、或5 B、或 C、或2 D、或26. 如图,点为▱的对称中心,轴,与轴交于点 , 与轴交于点 , , 若将绕点顺时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( )
A、或5 B、或 C、或2 D、或26. 如图,点为▱的对称中心,轴,与轴交于点 , 与轴交于点 , , 若将绕点顺时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( )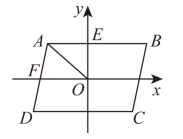 A、 B、 C、 D、7. 如图,在中,点 , 分别是 , 的中点,若 , 则( )
A、 B、 C、 D、7. 如图,在中,点 , 分别是 , 的中点,若 , 则( )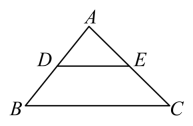 A、3 B、6 C、9 D、128. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( )
A、3 B、6 C、9 D、128. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在平行四边形中,E为的中点,交于F,若 , 则 .
 10. 如图,三角形纸片中, , 分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
10. 如图,三角形纸片中, , 分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 . 11. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.
11. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.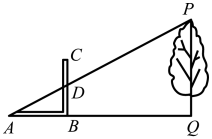 12. 如图,已知等腰三角形 于点 为 边中线, 相交于点 .在 从 减小到 的过程中,点 经过的路径长为 .
12. 如图,已知等腰三角形 于点 为 边中线, 相交于点 .在 从 减小到 的过程中,点 经过的路径长为 . 13. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 .
13. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 .
三、解答题
-
14. 如图,在矩形中,点在边上, , 垂足为F, , , , 求的长.
 15. 如图,在矩形中,于点E,点P是边上一点,且 . 求证: .
15. 如图,在矩形中,于点E,点P是边上一点,且 . 求证: .
四、综合题
-
16. 综合与实践.
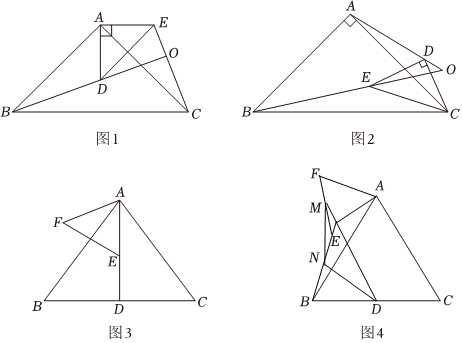 (1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .
(1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .的度数是 .
: .
(2)、类比探究如图 , 在和中, , 且 , , 连接、并延长交于点 .的度数是 ;
: .
(3)、问题解决如图 , 在等边中,于点 , 点在线段上不与重合 , 以为边在的左侧构造等边 , 将绕着点在平面内顺时针旋转任意角度如图 , 为的中点,为的中点.说明为等腰三角形.
求的度数.
17. 如图,在中,直线DF与边AB相交于点D,与边AC相交于点E,与线段BC延长线相交于点F. (1)、若 , , 求的值.(2)、若 , , 其中m>n>0,求的值.(3)、请根据上述(1)(2)的结论,猜想=(直接写出答案,不需要证明).
(1)、若 , , 求的值.(2)、若 , , 其中m>n>0,求的值.(3)、请根据上述(1)(2)的结论,猜想=(直接写出答案,不需要证明).