2023-2024学年初中数学九年级上册 25.5 相似三角形的性质同步分层训练基础卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $D E ∥ B C$ ， $E F ∥ A B$ ，则下列比例式中错误的是（）

A、 $\frac{D E}{B C} = \frac{A E}{E C}$ B、 $\frac{E F}{A B} = \frac{C E}{C A}$ C、 $\frac{C E}{C F} = \frac{C A}{C B}$ D、 $\frac{A D}{A B} = \frac{A E}{A C}$

查看试题解析
2. 如图， $A B ∥ C D$ ，若 $B O = 6$ ， $B D = 9$ ， $A B = 4$ ，则 $C D$ 的长是（）

A、 $\frac{1}{2}$ B、1 C、2 D、3

查看试题解析
3. 如图，AB∥CD，AD，BC相交于点O．若AB＝1，CD＝2，BO∶CO＝（）

A、1∶2 B、1∶4 C、2∶1 D、4∶1

查看试题解析
4. 如图，在△ABC中，DE∥BC，若 $\frac{A D}{D B} = \frac{1}{2}$ ，则△ADE与△ABC的面积之比为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
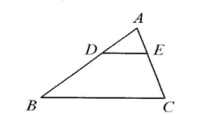5. 如图，在平行四边形ABCD中，E、F分别是边AB、CD的中点，BD分别交CE、AF于G、H，试判断下列结论：①△CBE≌△ADF；②CG＝AH；③ $B G = \frac{1}{2} G D$ ；④S_△_CBG＝2S_△_FHD ．其中正确的结论有（　　）个．

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，E、F是矩形ABCD的边AB上的两点，CE，DF相交于点O，已知△OCD面积为8， $△ O E F$ 面积为2，四边形AEOD的面积为5，则四边形BCOF的面积为（）

A、10 B、9 C、8 D、7

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = 3 ， B C = 4$ ，点 $D$ 在边 $A C$ 上，且 $B D$ 平分 $△ A B C$ 的周长，则 $B D$ 的长是（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、 $\frac{6 \sqrt{5}}{5}$ D、 $\frac{3 \sqrt{6}}{4}$

查看试题解析
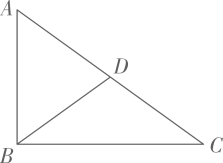8. “直角”在初中数学学习中无处不在在数学活动课上，李老师要求同学们用所学知识，利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角．甲、乙两名同学各自给出不同的作法，来判断∠AOB是不是直角
甲：如图1，在OA、OB上分别取点CD ，以C为圆心，CD长为半径画弧，交OB的反向延长线于点E ，若OE＝OD ，则∠AOB＝90°；

乙：如图2，在OA、OB上分别截取OM＝4个单位长度，ON＝3个单位长度，若MN＝5个单位长度，则∠AOB＝90°；

甲、乙两位同学作法正确的是（）

A、甲正确，乙不符合题意 B、乙正确，甲错误 C、甲和乙都错误 D、甲和乙都正确

查看试题解析

二、填空题

9. 如图， $D E / / B C$ ，若 $A D = 4$ ， $D B = 6$ ， $B C = 12$ ，则 $D E$ 的长为．

查看试题解析
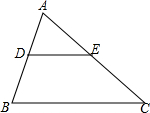10. 如图，△ABC中，点D、E分別在AB、AC上，DE∥BC，AD：DB＝1：2，则△ADE与△ABC的面积的比为.

查看试题解析
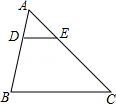11. 如图，已知两点A(2，0)，B(0，4)，且∠1＝∠2，则点C的坐标是

查看试题解析
12. 如图，在 $△ A B C$ 中， $A C = B C = 16$ ，点D在 $A B$ 上，点E在 $B C$ 上，点B关于直线 $D E$ 的轴对称点为点 $B^{'}$ ，连接 $D B^{'}$ ， $E B^{'}$ ，分别与 $A C$ 相交于F点，G点，若 $A F = 8 ， D F = 7 ， B^{'} F = 4$ ，则 $C G$ 的长度为．

查看试题解析
13. 如图，一束光线从点 $A (- 2 ， 5)$ 出发，经过y轴上的点 $B (0 ， 1)$ 反射后经过点 $C (m ， n)$ ，则 $2 m - n$ 的值是．

查看试题解析
14. 如图，在 $△ A B C$ 中，以点 $C$ 为圆心，任意长为半径作弧，分别交 $A C$ ， $B C$ 于点 $D$ ， $E$ ；分别以点 $D$ ， $E$ 为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧交于点 $F$ ；作射线 $C F$ 交 $A B$ 于点 $G$ ，若 $A C = 9$ ， $B C = 6$ ， $△ B C G$ 的面积为 $8$ ，则 $△ A C G$ 的面积为．

查看试题解析

三、解答题

15. 如图①， $△ A B C$ 和 $△ A D E$ 是等边三角形，连接 $D C$ ，点F，G，H分别是 $D E ， D C$ 和 $B C$ 的中点，连接 $F G ， F H$ ．易证： $F H = \sqrt{3} F G$ ．
若 $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形，且 $∠ B A C = ∠ D A E = 90 °$ ，如图②：若 $△ A B C$ 和 $△ A D E$ 都是等腰三角形，且 $∠ B A C = ∠ D A E = 120 °$ ，如图③：其他条件不变，判断 $F H$ 和 $F G$ 之间的数量关系，写出你的猜想，并利用图②或图③进行证明．

查看试题解析

16. 下面是小芸同学证明定理时使用的两种添加辅助线的方法，选择其中一种，完成证明．

定理：直角三角形斜边上的中线等于斜边的一半．已知：如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，点 $O$ 是 $A C$ 边的中点．

求证： $O B = \frac{1}{2} A C$ ．

方法一：

证明：延长 $B O$ 至 $D$ ，使 $O D = O B$ ，

连接 $A D$ ， $C D$ ．

方法二：

证明：过点 $O$ 作 $O D ⊥ B C$ 于点 $D$ ．

查看试题解析

四、综合题

17. 问题提出：已知矩形 $A B C D$ ，点 $E$ 为 $A B$ 上的一点， $E F ⊥ A B$ ，交 $B D$ 于点 $F$ ．将 $△ E B F$ 绕点 $B$ 顺时针旋转 $α$ $(0 ° <$ $α$ $< 90 °)$ 得到 $△$ $E^{'} B F^{'}$ ，则 $A E^{'}$ 与 $D F^{'}$ 有怎样的数量关系．

(1)、【问题探究】
探究一：如图，已知正方形 $A B C D$ ，点 $E$ 为 $A B$ 上的一点， $E F ⊥ A B$ ，交 $B D$ 于点 $F$ ．
如图1，直接写出 $\frac{D F}{A E}$ 的值；

(2)、将 $△ E B F$ 绕点 $B$ 顺时针旋转到如图 $2$ 所示的位置，连接 $A E$ 、 $D F$ ，猜想 $D F$ 与 $A E$ 的数量关系，并证明你的结论；

(3)、探究二：如图，已知矩形 $A B C D$ ，点 $E$ 为 $A B$ 上的一点， $E F ⊥ A B$ ，交 $B D$ 于点 $F$ ．

如图3，若四边形 $A B C D$ 为矩形， $\frac{A B}{B C} = \frac{\sqrt{2}}{2}$ ，将 $△ E B F$ 绕点 $B$ 顺时针旋转 $α （ 0 ° < α < 90 ° ）$ 得到 $△$ $E^{'} B F^{'}$ $(E$ 、 $F$ 的对应点分别为 $E^{'}$ 、 $F^{'}$ 点 $)$ ，连接 $A E^{'}$ 、 $D F^{'}$ ，则 $\frac{A E^{^{'}}}{D F^{^{'}}}$ 的值是否随着 $α$ 的变化而变化．若变化，请说明变化情况；若不变，请求出 $\frac{A E^{^{'}}}{D F^{^{'}}}$ 的值．

(4)、【一般规律】
如图3，若四边形 $A B C D$ 为矩形， $B C = m A B$ ，其它条件都不变，将 $△ E B F$ 绕点 $B$ 顺时针旋转 $α$ $(0 ° <$ $α$ $< 90$ $°)$ 得到 $△$ $E^{'} B F^{'}$ ，连接 $A E^{'}$ ， $D F^{'}$ ，请直接写出 $A E^{'}$ 与 $D F^{'}$ 的数量关系．

查看试题解析
18. 如图，在△ABC和△ADE中，∠DAB＝∠EAC，∠C＝∠E.

(1)、求证：AD·BC＝AB·DE；

(2)、若 $S_{△ A D E} ： S_{△ A B C} ＝ 4 ： 9 ， B C ＝ 6 ，$ 求DE的长.

查看试题解析

2023-2024学年初中数学九年级上册 25.5 相似三角形的性质 同步分层训练基础卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 25.5 相似三角形的性质同步分层训练基础卷(冀教版)