2023-2024学年初中数学九年级上册 25.4 相似三角形的判定 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使 , 则点所在的格点为( )
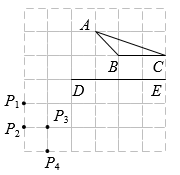 A、 B、 C、 D、2. 如图,能使成立的条件是( )
A、 B、 C、 D、2. 如图,能使成立的条件是( ) A、 B、 C、 D、3. 下列判断中,正确的是( )A、各有一个角是的两个等腰三角形相似 B、邻边之比为2:1的两个等腰三角形相似 C、各有一个角是的两个等腰三角形相似 D、邻边之比为2:3的两个等腰三角形相似4. 如图,在中,点D,E分别是 , 上的点,与交于点F,下列条件中不能使和相似的是( )
A、 B、 C、 D、3. 下列判断中,正确的是( )A、各有一个角是的两个等腰三角形相似 B、邻边之比为2:1的两个等腰三角形相似 C、各有一个角是的两个等腰三角形相似 D、邻边之比为2:3的两个等腰三角形相似4. 如图,在中,点D,E分别是 , 上的点,与交于点F,下列条件中不能使和相似的是( ) A、 B、 C、 D、5. 如图所示,网格中相似的两个三角形是( )
A、 B、 C、 D、5. 如图所示,网格中相似的两个三角形是( ) A、①与② B、①与③ C、③与④ D、②与③6. 如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于点F , 则图中共有相似三角形( )
A、①与② B、①与③ C、③与④ D、②与③6. 如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于点F , 则图中共有相似三角形( )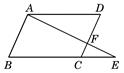 A、1对 B、2对 C、3对 D、4对7. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( )
A、1对 B、2对 C、3对 D、4对7. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( )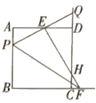 A、①②③ B、①③④ C、②③④ D、②④8. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A、①②③ B、①③④ C、②③④ D、②④8. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) A、(6,5) B、(6,0) C、(6,4) D、(4,2)
A、(6,5) B、(6,0) C、(6,4) D、(4,2)二、填空题
-
9. 如图,在中,点D在上,连接 . 请添加一个条件 , 使得 , 然后再加以证明.
 10. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对.
10. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对. 11. 如图,已知: , , ,当 的长为时, 与 相似.
11. 如图,已知: , , ,当 的长为时, 与 相似. 12. 如图: 中, 是AB边上一点(与AB不重合),过点 作直线截 ,所截得的三角形与原 相似,满足这样条件的直线共有条.
12. 如图: 中, 是AB边上一点(与AB不重合),过点 作直线截 ,所截得的三角形与原 相似,满足这样条件的直线共有条.
三、解答题
-
13. 如图,已知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
 (1)、当t为何值时,M为AB的中点。(2)、当t为何值时,△AMN为直角三角形.(3)、当t为何值时,△AMN是等腰三角形?并求此时点M的坐标。14. 已知在△ABC中,∠ABC=90°,AB=3cm,BC=4cm.动点Q从点A出发沿AC向终点C匀速运动,速度2cm/s;同时,点P从点B出发沿BA向终点A匀速运动,速度1cm/s;
(1)、当t为何值时,M为AB的中点。(2)、当t为何值时,△AMN为直角三角形.(3)、当t为何值时,△AMN是等腰三角形?并求此时点M的坐标。14. 已知在△ABC中,∠ABC=90°,AB=3cm,BC=4cm.动点Q从点A出发沿AC向终点C匀速运动,速度2cm/s;同时,点P从点B出发沿BA向终点A匀速运动,速度1cm/s;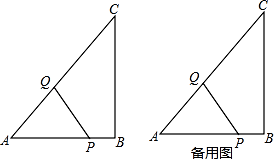 (1)、当t为何值时,△APQ与△ABC相似?
(1)、当t为何值时,△APQ与△ABC相似?
(2)、当t为何值时,△APQ为等腰三角形?四、作图题
-
15. 如图,图①、图②、图③均为4×2的正方形网格,△ABC的顶点均在格点上.按要求在图②、图③中各画一个顶点在格点上的三角形.
要求:

⑴所画的两个三角形都与△ABC相似但都不与△ABC全等.
⑵图②和图③中新画的三角形不全等.
五、综合题
-
16. 在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
 (1)、用含t的代数式表示:线段PO=cm;OQ=cm.(2)、当t为何值时△POQ的面积为6cm2?(3)、当△POQ与△AOB相似时,求出t的值.
(1)、用含t的代数式表示:线段PO=cm;OQ=cm.(2)、当t为何值时△POQ的面积为6cm2?(3)、当△POQ与△AOB相似时,求出t的值.
-

