2023-2024学年初中数学九年级上册 25.3 相似三角形同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 小明用放大镜观察一个三角形器材,并在纸上画出该三角形器材的示意图.通过测量发现,示意图的边长与实际器材的边长之比为 , 则示意图的面积与实际器材的面积之比为( )
 A、3:1 B、1:3 C、9:1 D、1:92. 如图,是等腰三角形, . 以点B为圆心,任意长为半径作弧,交AB于点F,交BC于点G,分别以点F和点G为圆心,大于的长为半径作弧,两弧相交于点H,作射线BH交AC于点D;分别以点B和点D为圆心,大于的长为半径作弧,两孤相交于M、N两点,作直线MN交AB于点E,连接DE.下列四个结论:①;②;③;④当时, . 其中正确结论的个数是( )
A、3:1 B、1:3 C、9:1 D、1:92. 如图,是等腰三角形, . 以点B为圆心,任意长为半径作弧,交AB于点F,交BC于点G,分别以点F和点G为圆心,大于的长为半径作弧,两弧相交于点H,作射线BH交AC于点D;分别以点B和点D为圆心,大于的长为半径作弧,两孤相交于M、N两点,作直线MN交AB于点E,连接DE.下列四个结论:①;②;③;④当时, . 其中正确结论的个数是( ) A、1 B、2 C、3 D、43. 已知两个相似三角形的面积之比为4:9,这两个三角形的周长的和是 , 那么较小的三角形的周长为( )A、 B、 C、 D、4. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( )
A、1 B、2 C、3 D、43. 已知两个相似三角形的面积之比为4:9,这两个三角形的周长的和是 , 那么较小的三角形的周长为( )A、 B、 C、 D、4. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( ) A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S45. 如图,将先向左平移4个单位,得到 , 再以原点O为位似中心,作的位似三角形 , 使它与的相似比为且在同一象限内,则点A的对应点的坐标是( )
A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S45. 如图,将先向左平移4个单位,得到 , 再以原点O为位似中心,作的位似三角形 , 使它与的相似比为且在同一象限内,则点A的对应点的坐标是( ) A、 B、 C、 D、6. 两个相似三角形,他们的周长分别是36和12.周长较大的三角形的最大边为15,周长较小的三角形的最小边为3,则周长较大的三角形的面积是( )A、52 B、54 C、56 D、587. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( )
A、 B、 C、 D、6. 两个相似三角形,他们的周长分别是36和12.周长较大的三角形的最大边为15,周长较小的三角形的最小边为3,则周长较大的三角形的面积是( )A、52 B、54 C、56 D、587. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( ) A、1个 B、2个 C、3个 D、0个8. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形,A、B、C的纸片的面积分别为S1、S2、S3 , (S1与S2 , S2与S3的相似比相同),相邻纸片之间互不重叠也无缝隙,若S1>S2>S3 , 则这个矩形的面积一定可以表示为( )
A、1个 B、2个 C、3个 D、0个8. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形,A、B、C的纸片的面积分别为S1、S2、S3 , (S1与S2 , S2与S3的相似比相同),相邻纸片之间互不重叠也无缝隙,若S1>S2>S3 , 则这个矩形的面积一定可以表示为( )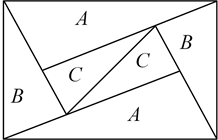 A、4S1 B、6S2 C、4S2+3S3 D、3S1+4S3
A、4S1 B、6S2 C、4S2+3S3 D、3S1+4S3二、填空题
-
9. 如图,在一个面积为的等边三角形纸片中,取三边的中点,以虚线为折痕折叠纸片,图中阴影部分的面积为.
 10. 如图,在矩形纸片中,将和分别沿和折叠(),点A,B重合于点E处;再将沿折叠,点C落在上的点F处,若 , 且 , 则的长为 .
10. 如图,在矩形纸片中,将和分别沿和折叠(),点A,B重合于点E处;再将沿折叠,点C落在上的点F处,若 , 且 , 则的长为 . 11. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
11. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 . 12. 如图,由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形 , 连接和 . 现随机向正方形内掷一枚小针,则针尖落在阴影区域的概率为 .
12. 如图,由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形 , 连接和 . 现随机向正方形内掷一枚小针,则针尖落在阴影区域的概率为 . 13. 如图,在平面直角坐标系中,矩形的边分别在x轴、y轴的正半轴上,点A的坐标为 , 点P在矩形的内部,点E在边上,且满足 , 当△是等腰三角形时,点P的坐标为 .
13. 如图,在平面直角坐标系中,矩形的边分别在x轴、y轴的正半轴上,点A的坐标为 , 点P在矩形的内部,点E在边上,且满足 , 当△是等腰三角形时,点P的坐标为 .
三、解答题
-
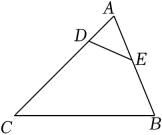
14. 已知的三边长分别为6,8,10,和相似的的最长边长为30,求的周长.15. 如图,分别是、上的点, , , , , , 求的长和的度数.
四、作图题
-
16. 图①、图②、图③都是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段的端点都在格点上,在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
 (1)、在图①中画 , 使;(2)、在图②中画 , 使是轴对称图形;(3)、在图③中画 , 使边上的高将分成面积比为的两部分.
(1)、在图①中画 , 使;(2)、在图②中画 , 使是轴对称图形;(3)、在图③中画 , 使边上的高将分成面积比为的两部分.五、综合题
-
17. 如图,在平面直角坐标系中,四边形OABC是正方形,点B坐标为(2 , 0),点D是射线OB上不与点O重合的一个动点,将线段CD绕点D顺时针旋转90°得到ED,连结AD、AE.
 (1)、求证:DA=DE;(2)、如图2,连结AC,BE,当△CDA与△DBE相似时,求BD的长;(3)、当点A关于直线ED的对称点A'落在正方形的边上时,求点D的坐标.18. 如图1,在平面直角坐标系中,点A、点B分别是x轴、y轴正半轴上的点,以OA、OB为边构造矩形OACB.点E为OA上一点,满足BE=BC.过点C作CF⊥BE,垂足为点F.已知 .
(1)、求证:DA=DE;(2)、如图2,连结AC,BE,当△CDA与△DBE相似时,求BD的长;(3)、当点A关于直线ED的对称点A'落在正方形的边上时,求点D的坐标.18. 如图1,在平面直角坐标系中,点A、点B分别是x轴、y轴正半轴上的点,以OA、OB为边构造矩形OACB.点E为OA上一点,满足BE=BC.过点C作CF⊥BE,垂足为点F.已知 .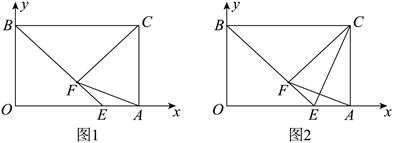 (1)、求证:CA=CF.(2)、如图2,连结CE,当∠BCF=2∠ECF时,求AE的长.(3)、在(2)的条件下,连结AF,在坐标平面内是否存在一点M,使得以点M、A、F为顶点的三角形与△CBE相似?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)、求证:CA=CF.(2)、如图2,连结CE,当∠BCF=2∠ECF时,求AE的长.(3)、在(2)的条件下,连结AF,在坐标平面内是否存在一点M,使得以点M、A、F为顶点的三角形与△CBE相似?若存在,请求出点M的坐标;若不存在,请说明理由.
-