2023-2024学年初中数学九年级上册 25.1 比例线段 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 已知P是线段的黄金分割点,且 , 那么的值为( )A、 B、 C、 D、2. 某品牌20寸的行李箱拉杆拉开后放置如图所示,经测量该行李箱从轮子底部到箱子上沿的高度与从轮子底部到拉杆顶部的高度之比是黄金比(约等于).已知cm,则AB约是( )
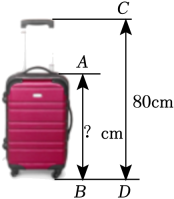 A、30cm B、49cm C、55cm D、129cm3. 如果 , 那么下列比例式中正确的是( )A、 B、 C、 D、4. 若 , 则下列式子不正确的是( )A、 B、 C、 D、5. 已知线段a、b,求作线段x,使 , 正确的作法是( )A、
A、30cm B、49cm C、55cm D、129cm3. 如果 , 那么下列比例式中正确的是( )A、 B、 C、 D、4. 若 , 则下列式子不正确的是( )A、 B、 C、 D、5. 已知线段a、b,求作线段x,使 , 正确的作法是( )A、 B、
B、 C、
C、 D、
D、 6. 已知非负数 x,y,z 满足. .,设 ,则 W 的最大值与最小值的和为( )A、-2 B、-4 C、-6 D、-87. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
6. 已知非负数 x,y,z 满足. .,设 ,则 W 的最大值与最小值的和为( )A、-2 B、-4 C、-6 D、-87. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )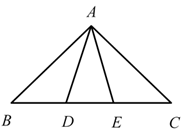 A、 B、 C、 D、8. 设 ,且 ,则 ( )A、673 B、 C、 D、674
A、 B、 C、 D、8. 设 ,且 ,则 ( )A、673 B、 C、 D、674二、填空题
-
9. 如图,用大小相同的小正方形拼图,第个图是一个小正方形;第个图由个小正方形拼成;第个图由个小正方形拼成,依此规律,若第个图比第个图多用了个小正方形,则的值是 .
 10. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比(即),可以增加视觉美感.如图,按此比例设计一座高度为的雕像,则该雕像的下部高度应设计为 m.(结果保留根号)
10. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比(即),可以增加视觉美感.如图,按此比例设计一座高度为的雕像,则该雕像的下部高度应设计为 m.(结果保留根号) 11. 生活中到处可见黄金分割的美.向日葵就是一个很好的例子,如果仔细观察向日葵中心,就会发现似乎有条螺旋形的曲线,如果对此进行计算,结果会得到黄金分割数列,如图是一株向日葵的俯视图,点C分线段AB近似于黄金分割(黄金分割比≈0.618).已知AC=2,且AC>BC,则BC的长约 .
11. 生活中到处可见黄金分割的美.向日葵就是一个很好的例子,如果仔细观察向日葵中心,就会发现似乎有条螺旋形的曲线,如果对此进行计算,结果会得到黄金分割数列,如图是一株向日葵的俯视图,点C分线段AB近似于黄金分割(黄金分割比≈0.618).已知AC=2,且AC>BC,则BC的长约 . 12. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .13. 若 , 则 的值为 .
12. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .13. 若 , 则 的值为 .三、解答题
-
14. 已知a、b、c分别是△ABC的三条边的边长,且a:b:c=5:7:8,3a-2b+c=9,求△ABC的周长.15. 阅读下列解题过程,然后解题:
题目:已知 互不相等),求 的值.
解:设 ,则 , ,
, .
依照上述方法解答下列问题:
已知 ,其中 ,求 的值.
四、综合题
-
16. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.
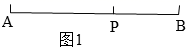
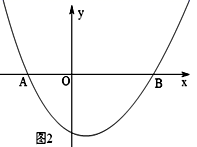 (1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.17. 如图1所示,点C把线段 分成 与 ,若 ,则称线段 被点C黄金分割(goldensection),点C叫做线段 的黄金分割点, 与 的比叫做黄金比.
(1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.17. 如图1所示,点C把线段 分成 与 ,若 ,则称线段 被点C黄金分割(goldensection),点C叫做线段 的黄金分割点, 与 的比叫做黄金比.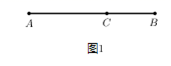 (1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C .
(1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C . (3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.
(3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.