2023-2024学年初中数学九年级上册 24.4 一元二次方程的应用 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题
-
1. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有64人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、 B、 C、 D、2. “读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )A、 B、 C、 D、3. 某超市购进一批商品,单价40元.经市场调查,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个,因受库存的影响,每批次进货个数不得超过180个,超市若将准备获利2000元,则定价为多少元?( )A、50 B、60 C、50或60 D、1004. 超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查,若每千克涨价1元,则日销售量减少20千克,如果超市要保证每天盈利6000元,则每千克应该涨价( )A、15元或20元 B、10元或15元 C、10元或20元 D、5元或10元5. 由于受猪瘟的影响,今年9月份猪肉的价格两次大幅上涨,瘦肉价格由原来每千克23元,连续两次上涨a%后,售价上升到每千克60元,则下列方程中正确的是( )A、23(1+a%)2=60 B、23(1-a%)2=60 C、23(1+2a%)=60 D、23(1+a2%)=606. 下列命题:① 若b=a+c时,一元二次方程一定有实数根;② 若方程有两个不相等的实数根,则方程也一定有两个不相等实数根;③ 若二次函数 , 当取、()时,函数值相等,则当x取时函数值为0;④ 若 , 则二次函数的图像与坐标轴的公共点的个数是2或3,其中正确结论的个数是( )A、1个 B、2个 C、3个 D、4个7. 已知 , , 是1,3,4中的任意一个数( , , 互不相等),当方程 的解均为整数时,以1,3和此方程的所有解为边长能构成的多边形一定是( )A、轴对称图形 B、中心对称图形 C、轴对称图形或中心对称图形 D、非轴对称图形或中心对称图形8. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
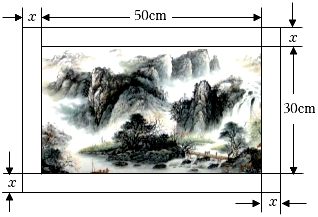
9. 如图所示,在一幅长、宽的风景画的四周镶一条金色纸边,制成一幅矩形挂图如图所示,如果要使整个矩形挂图的面积是 , 则金色纸边的宽为 cm.
 10. 如图,李大斧要建一个矩形羊圈,羊圈的一边利用长为的住房墙,另外三边用长的彩钢围成,为了方便进出,在垂直于住房墙的一边留了一扇宽的门.若要使羊圈的面积为 , 则所围矩形与墙垂直的一边长为 .
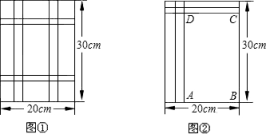
10. 如图,李大斧要建一个矩形羊圈,羊圈的一边利用长为的住房墙,另外三边用长的彩钢围成,为了方便进出,在垂直于住房墙的一边留了一扇宽的门.若要使羊圈的面积为 , 则所围矩形与墙垂直的一边长为 .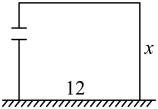 11. 方程x2-6x+8=0的两个根是等腰三角形的底和腰,则这个等腰三角形周长是 .12. 如图①:要设计一幅宽 , 长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
11. 方程x2-6x+8=0的两个根是等腰三角形的底和腰,则这个等腰三角形周长是 .12. 如图①:要设计一幅宽 , 长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?分析:由横、竖彩条的宽度比为2:3,可设每个横彩条的宽为 , 则每个竖彩条的宽为 . 为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形 .
结合以上分析完成填空:
如图②:用含的代数式表示:;;矩形的面积为;列出方程并完成本题解答.
 13. 如图,用120米长的围网围建一个面积为560平方米的矩形养殖场.为了节省材料,养殖场的一边靠墙(墙足够长),并在如图的两个位置各开出一个1米宽的门(门不用围网做).设矩形AB边长为x米,请依题意列方程: .
13. 如图,用120米长的围网围建一个面积为560平方米的矩形养殖场.为了节省材料,养殖场的一边靠墙(墙足够长),并在如图的两个位置各开出一个1米宽的门(门不用围网做).设矩形AB边长为x米,请依题意列方程: .
三、解答题
-
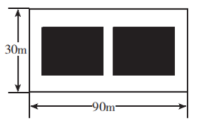
14. 随着互联网的发展,人们的购物方式有了变化,使用网络平台在线购物越来越多.某产品今年开始做线上销售,8月份的销售利润是6万元,10月份的销售利润是13.5万元,求9,10这两个月销售利润的月平均增长率.15. 某小区在绿化工程中有一块长为90m、宽为30m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
四、综合题
-
16. 如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
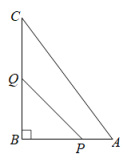 (1)、几秒后四边形APQC的面积是19平方厘米;(2)、若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.17. 商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.(1)、若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?(2)、在(1)的条件下,当这种背包销售单价为多少元时,销售利润是3120元?(3)、这种背包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.18. 有一块缺角矩形地皮ABCDE(如下图),其中AB=110m,BC=80m,CD=90m,∠EDC=135°,现准备用此地建一座地基为长方形(图中用阴影部分表示)的数学大楼,建筑公司在接受任务后,设计了A、B、C、D四种方案,请你研究探索应选用哪一种方案,才能使地基面积最大?
(1)、几秒后四边形APQC的面积是19平方厘米;(2)、若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.17. 商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.(1)、若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?(2)、在(1)的条件下,当这种背包销售单价为多少元时,销售利润是3120元?(3)、这种背包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.18. 有一块缺角矩形地皮ABCDE(如下图),其中AB=110m,BC=80m,CD=90m,∠EDC=135°,现准备用此地建一座地基为长方形(图中用阴影部分表示)的数学大楼,建筑公司在接受任务后,设计了A、B、C、D四种方案,请你研究探索应选用哪一种方案,才能使地基面积最大?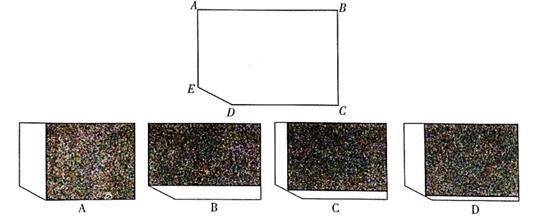 (1)、求出A、B两种方案的面积。(2)、若设地基的面积为S,宽为x,写出方案C(或D)中S与x的关系式。(3)、根据(2)完成下表
(1)、求出A、B两种方案的面积。(2)、若设地基的面积为S,宽为x,写出方案C(或D)中S与x的关系式。(3)、根据(2)完成下表地基的宽x ( m)
50
60
70
75
78
79
80
81
82
地基的面积(m2 )
(4)、根据上表提出你的猜测。(5)、用配方法对(2)中的S与x之间的关系式进行分析,并检验你的猜测是否正确。(6)、你认为A、B、C、D中哪一种方案合理?