2023-2024学年初中数学九年级上册 24.2 解一元二次方程同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 若关于x的一元二次方程 ( k-2)x²-2x+1=0有两个不相等的实数根，且k为非负整数，则符合条件的k的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 已知一元二次方程 $x^{2} + 4 x - 3 = 0$ ，下列配方正确的是（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 7$ D、 ${(x - 2)}^{2} = 7$

查看试题解析
3. 方程 ${(x - 2)}^{2} = 3 (x - 2)$ 的解是（）

A、 $x = 2$ B、 $x = 3$ C、 $x_{1} = 2$ ， $x_{2} = 3$ D、 $x_{1} = 2$ ， $x_{2} = 5$

查看试题解析
4. 关于x的方程 $x^{2} + m x - m^{2} = - 5$ 的一个根是4，那么m的值是（）

A、-3或4 B、 $- 3$ 或7 C、3或4 D、3或7

查看试题解析
5. 方程 $x^{2} = x$ 的解是（）

A、 $x_{1} = 3$ ， $x_{2} = - 3$ B、 $x_{1} = 1$ ， $x_{2} = 0$ C、 $x_{1} = 1$ ， $x_{2} = - 1$ D、 $x_{1} = 3$ ， $x_{2} = - 1$

查看试题解析
6. 一元二次方程 $x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
7. 已知关于x的一元二次方程 $(p + 1) x^{2} + 2 q x + (p + 1) = 0$ （其中p，q为常数）有两个相等的实数根，则下列结论中，错误的是（）．

A、1可能是方程 $x^{2} + q x + p = 0$ 的根 B、-1可能是方程 $x^{2} + q x + p = 0$ 的根 C、0可能是方程 $x^{2} + q x + p = 0$ 的根 D、1和-1都是方程 $x^{2} + q x + p = 0$ 的根

查看试题解析
8. 对于题目“一段抛物线L： $y = - x^{2} - 5 x + c (- 5 \leq x \leq 0)$ 与直线l： $y = - x + 5$ 有唯一公共点.若c为整数，确定所有c的值.”甲的结果是 $c = 1$ ，乙的结果是 $2 \leq c \leq 5$ 的整数，丙的结果是 $6 \leq c \leq 10$ 的整数，则（）

A、甲、乙的结果合在一起才正确 B、乙、丙的结果合在一起才正确 C、甲、丙的结果合在一起才正确 D、甲、乙、丙的结果合在一起才正确

查看试题解析

二、填空题

9. 若一元二次方程 $x^{2} + m x + 2 = 0$ 有两个相等的实数根，则 $m$ 的值是.

查看试题解析
10. 已知关于 $x$ 的一元二次方程 $a x^{2} + x + c = 0$ 的两根为 $- 1$ 、 $2$ ，则方程 $c x^{2} - x + a = 0$ 的两根为.

查看试题解析
11. 关于x的方程kx²+（k+1）x+k﹣1＝0的根为整数，则实数k=.

查看试题解析
12. 在平面直角坐标系中点A（0，6）、B（6，0），AC、BD分别垂直于y轴、x轴，CA＝3，∠COD＝45°，二次函数y＝﹣ $\frac{1}{8}$ x²+m与线段CD有两个公共点时，m的取值范围是.

查看试题解析
13. 如图是一块矩形菜地ABCD，AB=a（m），AD=b（m），面积为 $s (m^{2})$ .现将边AB增加1m.

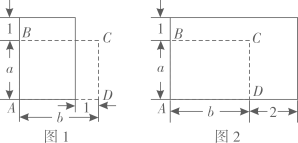(1)、如图1，若a=5，边AD减少1m，得到的矩形面积不变，则b的值是.

(2)、如图2，若边AD增加2m，有且只有一个a的值，使得到的矩形面积为 $2 s (m^{2})$ ，则s的值是.

查看试题解析

三、解答题

14. 请你先认真阅读下列材料，再参照例子解答问题：
已知 $(x + y - 3) (x + y + 4) = - 10$ ，求 $x + y$ 的值；
解：设 $x + y = t$ ，则原方程可变形为 $(t - 3) (t + 4) = - 10$ .即 $t^{2} + t - 2 = 0$
∴ $(t + 2) (t - 1) = 0$ 得 $t_{1} = - 2$ ， $t_{2} = 1$
∴ $x + y = - 2$ 或 $x + y = 1$
已知 $(x^{2} + y^{2} - 2) (x^{2} + y^{2} - 3) = 12$ ，求 $x^{2} + y^{2}$ 的值.

查看试题解析
15. 阅读下面的材料，解答问题．
材料：解含绝对值的方程： $x^{2} - 3 | x | - 10 = 0$ ．

解：分两种情况：

①当 $x \geq 0$ 时，原方程化为 $x^{2} - 3 x - 10 = 0$ ，解得 $x_{1} = 5$ ， $x_{2} = - 2$ （舍去）；

②当 $x < 0$ 时，原方程化为 $x^{2} + 3 x - 10 = 0$ ，解得 $x_{3} = - 5$ ， $x_{4} = 2$ （舍去）．

综上所述，原方程的解是 $x_{1} = 5$ ， $x_{2} = - 5$ ．

请参照上述方法解方程 $x^{2} - | x + 1 | - 1 = 0$ ．

查看试题解析

四、综合题

16. 等腰△ABC的直角边AB＝BC＝10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q在BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t，△PCQ的面积为S．

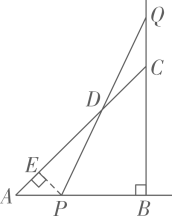(1)、求出S关于t的函数关系式；

(2)、当点P运动几秒时，S_△_PCQ＝S_△_ABC？

(3)、作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．

查看试题解析

17. 关于x的一元二次方程

x^{2} + b x + c = 0

经过适当变形，可以写成

(x - s) (x - t) = p (s \leq t)

的形式．现列表探究

x^{2} - 4 x - 5 = 0

的变形：

变形	s	t	p
$(x + 1) (x - 5) = 0$	-1	5	0
$x (x - 4) = 5$	0	4	5
$(x - 1) (x - q) = 8$	1	q	8
${(x - 2)}^{2} = 9$	2	2	9

回答下列问题：

(1)、表格中q的值为．

(2)、观察上述探究过程，表格中s与t满足的等量关系为．

(3)、记

x^{2} + b x + c = 0

的两个变形为

(x - s_{1}) (x - t_{1}) = p_{1}

和

(x - s_{2}) (x - t_{2}) = p_{2} (p_{1} \neq p_{2})

，求

\frac{t_{1} - t_{2}}{s_{1} - s_{2}}

的值．

查看试题解析

2023-2024学年初中数学九年级上册 24.2 解一元二次方程 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 24.2 解一元二次方程同步分层训练培优卷(冀教版)