2023-2024学年初中数学九年级上册 24.1 一元二次方程同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 已知方程x²-4x+k＝0的两个实数根是x₁＝1，x₂＝3，则方程（x-5）²-4（x-5）+k＝0的两个实数根是（　　）

A、x₁＝1，x₂＝3 B、x₁＝6，x₂＝8 C、x₁＝-4，x₂＝-2 D、x₁＝0，x₂＝2

查看试题解析
2. 据乘用车市场信息联席会数据显示，我国新能源车发展迅速，2023年1月至3月，新能源车月销量由 $33.2$ 万辆增加到 $54.6$ 万辆．设2023年1月至3月新能源车销量的月平均增长率为x，则列（）

A、 $33.2 (1 + 2 x) = 54.6$ B、 $33.2 \times 2 \cdot (1 + x) = 54.6$ C、 $33.2 [1 + (1 + x) + {(1 + x)}^{2}] = 54.6$ D、 $33.2 {(1 + x)}^{2} = 54.6$

查看试题解析
3. 某学校连续三年组织学生参加义务植树活动，第一年植树400棵，第三年植树625棵，设该校植树棵数的年平均增长率为 $x$ ，下列方程正确的是（）

A、 $400 (1 + x)^{2} = 625$ B、 $400 (1 - x)^{2} = 625$ C、 $625 (1 + x)^{2} = 400$ D、 $625 (1 - x)^{2} = 400$

查看试题解析
4. 杭州地铁 $3$ 号线于2022年2月21日实现试运行，从星桥站至潮王路站共设计了1482种往返车票，则这段线路有多少个站点？设这段线路有 $x$ 个站点，根据题意下面列出的方程正确的是（）

A、 $x (x + 1) = 1482$ B、 $x (x - 1) = 1482$ C、 $\frac{1}{2} x (x + 1) = 1482$ D、 $\frac{1}{2} x (x - 1) = 1482$

查看试题解析
5. 下列说法正确的是（）

A、五边形的外角和是540° B、对角线相等且互相垂直的四边形是正方形 C、因式分解 $2 a^{2} - a b - a = 2 a (a - b - 1)$ 是正确的 D、关于x的方程 $- x^{2} + b x + 1 = 0$ 有两个不相等的实数根

查看试题解析
6. 设a，b是方程 $x^{2} + x - 2023 ＝ 0$ 的两个实数根，则 $a^{2} + 2 a + b$ 的值为（）

A、2024 B、2021 C、2023 D、2022

查看试题解析
7. 已知 $\frac{a^{2} - c}{a} - 1 = 0$ ， $\frac{b^{2} - c}{b} - 1 = 0$ ，若 $a \neq b$ ，则下列等式成立的是（）

A、 $a + b = - 1$ B、 $a + b = 1$ C、 $a - b = 1$ D、 $a - b = - 1$

查看试题解析
8. 如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

9. 若关于x的一元二次方程x²+ax+2a+3=0的一个根是1，则a的值是.

查看试题解析
10. 某网络学习平台2020年底的新注册用户数为100万，到2022年底的新注册用户数达到169万，设新注册用户数的年平均增长率为x，则可列出关于x的方程为．

查看试题解析
11. 若关于 $x$ 的一元二次方程 $a x^{2} + b x - 1 = 0$ 有一个根为 $- 2$ ，则 $2 a - b =$ ．

查看试题解析
12. 等腰三角形的三边的长是a 、b、4，其中a、b是方程x²-6x+c=0两个根，则此三角形的三边长是．

查看试题解析
13. 如果关于x的一元二次方程ax²＋bx＋c＝0有两个实数根x₁ ， x₂ ，且满足数轴上x₁ ， x₂所表示的点到2所表示的点的距离相等，则称这样的方程为“关于2的等距方程”以下“关于2的等距方程”的说法，正确的有．（填序号）
①方程x²﹣4x＝0是关于2的等距方程；

②当5m＝﹣n时，关于x的方程（x＋1）（mx＋n）＝0一定是关于2的等距方程；

③若方程ax²＋bx＋c＝0是关于2的等距方程，则必有b＝﹣4a（a≠0）；

④当两根满足x₁＝3x₂ ，关于x的方程px²﹣x $+ \frac{3}{4} =$ 0是关于2的等距方程．

查看试题解析

三、解答题

14. 关于x的一元二次方程2（x-1）²+b（x-1）+c＝0化为一般形式后为2x²-3x-1＝0，试求b，c的值．

查看试题解析
15. 若a是方程x²﹣2018x+1＝0的一个根，求代数式a²﹣2019a+ $\frac{a^{2} + 1}{2018}$ 的值．

查看试题解析

四、综合题

16. 在平面直角坐标系中，矩形 $O A B C$ 的边 $O A$ 、 $O C$ 分别在x轴的正半轴、y轴的正半轴上，且 $O A$ 、 $O C$ 的长是方程 $x^{2} - 20 x + 100 = 0$ 的两个根．

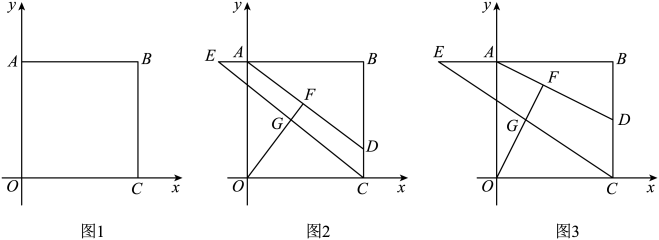(1)、如图1，求点C坐标；

(2)、如图2，点D在 $C B$ 上，点E在 $B A$ 的延长线上，且 $C D = A E$ ．连接 $A D 、 C E$ ，过点O作 $O F ⊥ A D$ 交 $C E$ 于点G，垂足为点F．设 $C D$ 长为m，点G的横坐标为n，求n与m的函数关系式（不要求写出自变量m的取值范围）；

(3)、如图3，在（2）的条件下，当 $F G ： G O = 3 ： 5$ 时，求直线 $A D$ 的解析式．

查看试题解析
17. 如图，在平面直角坐标系中，直线AB交y轴于点A，交x轴于点B，OA，OB（ $O A < O B$ ）的长是关于x的一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，直线 $x = 2$ 交AB于点D，交x轴于点E，P是直线 $x = 2$ 上一动点，设 $P (2 ， n)$ ．

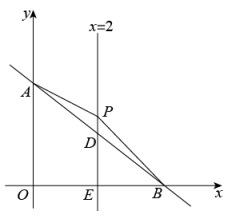(1)、求直线AB的解析式；

(2)、设 $△ A B P$ 的面积为S（ $S \neq 0$ ），求S关于n的函数关系式，并写出自变量n的取值范围；

(3)、在（2）的条件下，当 $S = 1$ ，且点P在AB上方时，在第一象限是否存在点C，使 $△ P B C$ 是等腰直角三角形？若存在，请直接写出点C的坐标；若不存在，请说明理由．

查看试题解析

2023-2024学年初中数学九年级上册 24.1 一元二次方程 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 24.1 一元二次方程同步分层训练培优卷(冀教版)