2023-2024学年初中数学九年级上册 23.4 用样本估计总体同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 某校对八年级各班进行卫生大评比，10个班的成绩汇总统计后制成如下表格：

平均数

众数

中位数

方差

9.3

9.2

9.4

0.2

学校规定该年级卫生评比要求：去掉一个最高分，去掉一个最低分后进行统计评比．则去掉最高和最低的两个分数后，表中相关的数据一定不发生变化的是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
2. 八年级一班今年的平均年龄是12.5岁，方差是40，一年后该班学生全员升到九年级时，下列说法正确的是（）

A、平均年龄不变 B、年龄的方差不变 C、年龄的众数不变 D、年龄的中位数不变

查看试题解析
3. 某果园实验基地种植了甲、乙两个品种的葡萄树，工作人员随机从甲、乙两品种的葡萄树中采摘了10棵，统计了每棵的产量.下列关于两品种每棵产量的平均数和方差的描述中，能说明甲品种的葡萄产量较稳定的是（）

A、 ${\bar{x}}_{甲} > {\bar{x}}_{乙}$ B、 ${\bar{x}}_{甲} < {\bar{x}}_{乙}$ C、 $S_{甲}^{2} < S_{乙}^{2}$ D、 $S_{甲}^{2} > S_{乙}^{2}$

查看试题解析
4. 为了调查八年级学生完成家庭作业所需的时间，在某校抽查了8名学生，他们每天完成作业所需的时间分别为（单位：分）：70，75，90，70，70，58，80，55，则这组数据的众数、中位数、平均数依次是（）

A、70，70，71； B、70，71，70； C、71，70，70； D、70，70，70

查看试题解析
5. 某养殖专业户为了估计其皖鱼养殖池中鲩鱼的数量，第一次随机捕捞了36条鲩鱼，将这些鱼一一做好标记后放回池塘中．一周后，从池塘中捕捞了750条鱼，其中有标记的鲩鱼共2条，估计该池塘中鲩鱼的数目为（）

A、54000 B、27000 C、13500 D、6750

查看试题解析
6. 从某奶茶小店某月每日营业额（单位：元）中随机抽取部分数据进行整理分析，根据方差公式，得 $s^{2} = \frac{1}{n} [{(200 - \bar{x})}^{2} \times 3 + {(300 - \bar{x})}^{2} \times 5 + {(400 - \bar{x})}^{2} + {(500 - \bar{x})}^{2}]$ ．则下列说法正确的是（）

A、样本容量是4 B、该组数据的中位数是400 C、该组数据的众数是400 D、 $s^{2} = 8000$

查看试题解析
7. 某校积极鼓励学生参加志愿者活动，下表列出了随机抽取的 $100$ 名学生一周参与志愿者活动的时间情况：
参与志愿者活动的时间（h）
1
$1.5$
2
$2.5$
3
参与志愿者活动的人数（人）
$20$
x
$38$
8
2
根据表中数据，下列说法中错误的是（）

A、表中 $x$ 的值为 $32$ B、这组数据的众数是 $2 h$ C、这组数据的中位数是 $2 h$ D、这组数据的平均数是 $1.7 h$

查看试题解析

二、填空题

8. 甲、乙两名学生参加学校举办的“歌手大赛”.两人5次成绩的平均数都是95分，方差分别是 $s_{甲}^{2} = 2.5 ， s_{乙}^{2} = 3$ ，则两人成绩比较稳定的是.(填“甲”或“乙”)

查看试题解析
9. 某校为了解学生对A，B，C，D四类运动的参与情况，随机调查了本校80名学生，让他们从中选择参与最多的一类，得到对应的人数分别是30，20，18，12．若该校有800名学生，则估计有人参与A类运动最多．

查看试题解析
10. 质检部门从甲，乙两个厂家生产的同一种产品中，各抽出8件产品，对其使用寿命进行跟踪调查，结果如下（单位：年）
甲：3，4，5，6，7，7，8，8；乙：4，6，6，6，8，9，12，13．
已知两个厂家在广告中都称该种产品的使用寿命是6年．请根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一种特征数？
甲：，乙：．

查看试题解析
11. 2022年10月12日，“天宫课堂”第三课在问天实验舱内开讲．进行的太空实验有①毛细效应；②水球变“懒”实验；③太空趣味饮水；④会调头的扳手．某校1500名学生在线观看了“天宫课堂”第三课，并参与了关于“我最喜爱的太空实验”的问卷调查．如果从中随机抽取45名学生的问卷调查情况进行统计分析，并将调查数据整理成下面的条形图，那么估计该校喜欢③太空趣味饮水实验的初中学生有名．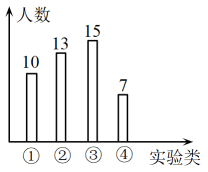

查看试题解析

三、解答题

12.
某体院要了解篮球专业学生投篮的命中率，对学生进行定点投篮测试，规定每人投篮20次，测试结束后随机抽查了一部分学生投中的次数，并分为五类，Ⅰ：投中11次；Ⅱ投中12次；Ⅲ：投中13次；Ⅳ：投中14次；Ⅴ：投中15次．根据调查结果绘制了下面尚不完整的统计图1、图2：
回答下列问题：
（1）本次抽查了名学生，图2中的m= ．
（2）补全条形统计图，并指出中位数在哪一类．
（3）求最高的命中率及命中最高的人数所占的百分比．
（4）若体院规定篮球专业学生定点投篮命中率不低于65%记作合格，估计该院篮球专业210名学生中约有多少人不合格．

查看试题解析

四、综合题

13. 2022年5月5日中国共产主义青年团成立100周年，某校开展“赓继红色血脉，敬致百年风华”系列活动．在活动前某校团委随机抽取部分学生调查其对“共青团”的了解情况，并将了解程度由高到低分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．对调查结果整理后绘制了如下两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

(1)、被调查学生的人数为．

(2)、补全条形统计图．

(3)、在扇形统计图中的“C．基本了解”对应的扇形圆心角的度数为．

(4)、已知该校有800名学生，估计对“共青团”知识了解程度达到“C．基本了解”及以上的学生有多少人．

查看试题解析
14. 山西某中学王老师为了选拔一名优秀的学生参加市内的数学比赛，对两名备赛选手进行了6次测验，两位同学的测验成绩如表所示：
（参考公式 $S^{2} = \frac{(x_{1} - \bar{x})^{2} + (x_{2} - x)^{2} + ⋯ + (x_{n} - \bar{x})^{2}}{n}$ ）

第1次
第2次
第3次
第4次
第5次
第6次
平均成绩
中位数
众数
方差
甲
83
85
90
80
85
87
85
a
85
b
乙
86
86
83
84
85
86
c
85.5
d
$\frac{4}{3}$
根据表中提供的数据，解答下列问题：

(1)、a的值为， d的值为．

(2)、求b和c的值，并直接指出哪位同学的成绩更稳定．

(3)、根据以上信息，你认为王老师应该选哪位同学参加比赛，请说明理由．

查看试题解析
15. 6月的第三个星期天是父亲节，某校组织了以“父爱如山”为主题的演讲比赛，根据初赛成绩，七、八年级各选出 $5$ 名学生组成代表队，参加决赛．并根据他们的决赛成绩绘制了如下两幅统计图表：(满分为 $100$ 分)

(1)、补全下表中的数据；
组别
平均数(分)
中位数(分)
众数(分)
七年级
$85$
八年级
$85$
$100$

(2)、结合两队决赛成绩的平均数和中位数，评价两个队的决赛成绩；

(3)、哪个年级代表队的决赛成绩更稳定．

查看试题解析

参与志愿者活动的时间（h）	1	$1.5$	2	$2.5$	3
参与志愿者活动的人数（人）	$20$	x	$38$	8	2

	第1次	第2次	第3次	第4次	第5次	第6次	平均成绩	中位数	众数	方差
甲	83	85	90	80	85	87	85	a	85	b
乙	86	86	83	84	85	86	c	85.5	d	$\frac{4}{3}$

组别	平均数(分)	中位数(分)	众数(分)
七年级		$85$
八年级	$85$		$100$

平均数	众数	中位数	方差
9.3	9.2	9.4	0.2

2023-2024学年初中数学九年级上册 23.4 用样本估计总体 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 23.4 用样本估计总体同步分层训练培优卷(冀教版)