2023-2024学年初中数学九年级上册 23.3 方差同步分层训练基础卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 某中学青年志愿者协会的

10

名志愿者，一周的社区志愿服务时间如表所示：

时间 $/ h$	$2$	$3$	$4$	$5$	$6$
人数	$1$	$3$	$2$	$3$	$1$

关于志愿者服务时间的描述正确的是（）

A、众数是

6

B、中位数是

4

C、平均数是

3

D、方差是

1

查看试题解析

2. 甲和乙一起练习射击，第一轮10枪打完后两人的成绩如图所示．设他们这10次射击成绩的方差为S_甲²、S_乙² ，下列关系正确的是（）

A、S_甲²＜S_乙² B、S_甲²＞S_乙² C、S_甲²=S_乙² D、无法确定

查看试题解析
3. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

甲
乙
丙
丁
平均数 $(c m)$
          $185$
          $180$
          $185$
          $180$
方差
          $3.6$
          $3.6$
          $7.4$
          $8.1$

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 小明所在班级10名同学的身高（単位：cm）数据如下：165，158，168，162，174，168，162，165，168，170．下列统计量中，能够描述这组数据离散程度的是（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
5. 数据3，2，0，1， $- 1$ 的方差等于（）

A、0 B、1 C、2 D、3

查看试题解析
6. 下图是2019年5月17日至31日某市的空气质量指数趋势图．

（说明：空气质量指数为0－50、51－100、101－150分别表示空气质量为优、良、轻度污染）

有如下结论：

①在此次统计中，空气质量为优的天数少于轻度污染的天数；

②在此次统计中，空气质量为优良的天数占 $\frac{4}{5}$ ；

③20，21，22三日的空气质量指数的方差小于26，27，28三日的空气质量指数的方差．

上述结论中，所有正确结论的序号是（）

A、① B、①③ C、②③ D、①②③

查看试题解析
7. 一组数据a－1、b－1、c－1、d－1、e－1、f－1、g－1的平均数是m，方差是n，则另一组数据2a－3、2b－3、2c－3、2d－3、2e－3、2f－3、2g－3的平均数和方差分别是（）

A、2m－3、2n－3 B、2m－1、4n C、2m－3、2n D、2m－3、4n

查看试题解析
8. 若 $x_{1} ， x_{2} ， x_{3}$ 的方差为5，则 $x_{1} + 1$ ， $x_{2} + 1$ ， $x_{3} + 1$ 的方差为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 若样本数据3、6、a、4、2的平均数是4，则其方差是

查看试题解析
10. 甲、乙、丙、丁四名同学进行跳远测试，每人 $10$ 次跳远成绩的平均数都是 $2.68 m$ ，方差分别是 $S_{甲}^{2} = 1.60$ ， $S_{乙}^{2} = 1.62$ ， $S_{丙}^{2} = 0.58$ ， $S_{丁}^{2} = 0.45$ ，则这四名同学跳远成绩最稳定的是．

查看试题解析

11. 为备战东营市第十二届运动会，某县区对甲、乙、丙、丁四名射击运动员进行射击测试，他们射击测试成绩的平均数

\bar{x}

（单位：环）及方差

S^{2}

（单位：环²）如下表所示：

	甲	乙	丙	丁
$\bar{x}$	$9.6$	$8.9$	$9.6$	$9.6$
$S^{2}$	$1.4$	$0.8$	$2.3$	$0.8$

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择．

查看试题解析

12. 2022年9月起，劳动课正式成为中小学的一门独立课程．某班为了选拔一名学生参加学校组织的以“热爱劳动励心智，品味生活促成长”为主题的展示活动，在班里组织了6项活动，分别是煮饭烧菜、收纳物品、种植植物、修理家电、打扫卫生、和面蒸馍．其中甲、乙两名学生较为突出，他们在6项活动中的成绩（单位：分）如表所示：
甲
12.1
12.1
12.0
11.9
11.8
12.1
乙
12.2
12.0
11.8
12.0
12.3
11.7
由于甲、乙两名学生成绩的平均数相同，班级决定依据他们成绩的稳定性进行选拔，那么被选中的是同学．

查看试题解析

三、解答题

13. 学校运动会开设了“抢收抢种”项目，八(5)班甲，两个队伍都想代表班级参赛，为了选择一个比较好的队伍，八(5)班的班委组织了一次选拔赛，甲，乙两队各5人的比赛成绩如下表(单位：分)：

甲队

7

8

10

7

9

乙对

7

8

7

9

9

经计算，甲队比赛成绩的平均数为8分，方差为1.2，请计算乙队比赛成绩的方差，并根据计算结果，帮助班委选择一个成绩比较稳定的队伍代表班级参赛.

查看试题解析

14. 根据以下素材，探索完成“问题解决”中的任务1和任务2.

让学生了解班级粮食浪费现状，体会浪费粮食的危害

背景

为了解落实“光盘行动”的情况，某校同学调研了七、八年级部分班级某一天的餐厨垃圾质量．

素材1

从七、八年级中随机抽取了10个班的餐厨垃圾质量，数据如下（单位： $k g$ ）

七年级	$0.8$	$0.9$	$0.8$	$0.8$	$1.1$	$1.7$	$2.3$	$1.1$	$1.9$	$1.6$
八年级	$1.0$	$\begin{array}{l} 0.9 \end{array}$	$\begin{array}{l} 1.3 \end{array}$	$1.0$	$1.9$	$1.0$	$\begin{array}{l} 0.9 \end{array}$	$\begin{array}{l} 1.7 \end{array}$	$\begin{array}{l} 2.3 \end{array}$	$1.0$

素材2

餐厨垃圾质量用x表示，分四个等级：

A： $x < 1$ ；

B： $1 \leq x < 1.5$ ；

C： $1.5 < x < 2$ ；

D： $x \geq 2$ ．

（备注：餐厨垃圾质量越小，说明光盘行动落实越到位）

素材3

七八年级抽取的班级餐厨垃圾数据分析表

年级	平均数	中位数	众数	方差	A等级所占百分比
七年级	a	$1.1$	$0.8$	$\begin{array}{l} 0.26 \end{array}$	$40 %$
八年级	$1.3$	b	$1.0$	$\begin{array}{l} 0.22 \end{array}$	c

问题解决

任务1

数据处理

（1）求出素材3表格中的a，b，c的值；

任务2

数据分析

（2）根据以上数据，你认为该校七、八年级的“光盘行动”，哪个年级落实得更好，请说明理由（写出一条理由即可）．

查看试题解析

四、综合题

15. 我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．

	平均分 $（$ 分 $）$	中位数 $（$ 分 $）$	众数 $（$ 分 $）$	方差（ $分^{2}$ ）
初中部	$a$	$85$	$b$	$S_{初中}^{2}$
高中部	$85$	$c$	$100$	$160$

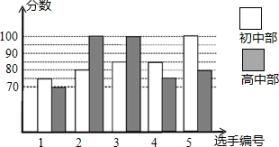(1)、根据图示计算出

a

、

b

、

c

的值；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算初中代表队决赛成绩的方差

s_{初 中}^{2}

，并判断哪一个代表队选手成绩较为稳定．

查看试题解析

16. 为了解 $A$ 、 $B$ 两家酒店的经营状况，获得了它们去年下半年7~12月的月营业额（单位：百万元）的数据，并对数据进行整理和分析.下面给出了两条信息：① $A$ 、 $B$ 两家酒店去年7~12月月营业额的平均数、中位数、方差；② $A$ 、 $B$ 两家酒店去年7~12月月营业额折线统计图.

平均数（百万元）
中位数（百万元）
方差（百万元）
          $A$ 酒店
2.5
2.45
1.073
          $B$ 酒店
          $m$
          $n$
0.54
根据以上信息，回答下列问题：

(1)、直接写出表中 $m$ 、 $n$ 的值；

(2)、根据所得信息，你认为哪家酒店经营状况较好？请简述理由.

查看试题解析