2023-2024学年初中数学九年级上册 23.2 中位数与总数 同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 某校举行“喜迎二十大”党史知识竞赛，如图是10名决赛选手的成绩，对于这10名选手的成绩，下列说法中正确的是（ ）

     

    A、众数是5 B、众数是2 C、中位数是95 D、中位数是90

    查看试题解析

  • 2. 长沙市某一周内每日最高气温的情况如图所示，下列说法中错误的是（　　）

      

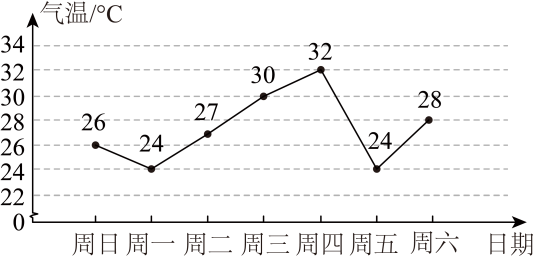    A、这周最高气温是32℃ B、这组数据的中位数是30 C、这组数据的众数是24 D、周四与周五的最高气温相差8℃

    查看试题解析

  • 3. 若一组数据1 ， 3 ， 4 ， 6 ， m的平均数为4 ， 则这组数据的中位数和众数分别是（ ）
    A、4 ， 4 B、4 ， 6 C、3 ， 6 D、3 ， 4

    查看试题解析

  • 4. 徐州云龙山共九节，蜿蜒起伏，形似游龙，每节山的海拔如图所示．

    其中，海拔为中位数的是（ ）

    A、第五节山 B、第六节山 C、第八节山 D、第九节山

    查看试题解析

  • 5. 绥化市举办了2023年半程马拉松比赛，赛后随机抽取了部分参赛者的成绩（单位：分钟），并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是（  ）                                                                                                                                                                          

    组别

    参赛者成绩

    A

             70⩽x<80

    B

             80⩽x<90

    C

             90⩽x<100

    D

             100⩽x<110

    E

             110⩽x<120

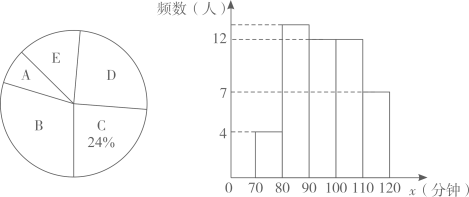    A、该组数据的样本容量是50人 B、该组数据的中位数落在90~100这一组 C、90~100这组数据的组中值是96 D、110~120这组数据对应的扇形统计图的圆心角度数为51°

    查看试题解析

  • 6. 申报某个项目时，某7个区域提交的申报表数量的前5名的数据统计如图所示，则这7个区域提交该项目的申报表数量的中位数是（    ）

      

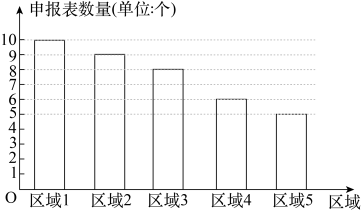    A、8 B、7 C、6 D、5

    查看试题解析

  • 7. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（  ）
    A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大

    查看试题解析

  • 8. 我们把三个数的中位数记作Z{a，b，c}．例如Z{1，3，2}＝2．函数y＝|2x+b|的图象为C1 ， 函数y＝Z{x+1，﹣x+1，3}的图象为C2 ． 图象C1在图象C2的下方点的横坐标x满足﹣3＜x＜1，则b的取值范围为（   ）
    A、0＜b＜3 B、b＞3或b＜0 C、0≤b≤3 D、1＜b＜3

    查看试题解析

二、填空题

  • 9. 某工厂第一车间有15名工人，每人日均加工螺杆数统计如图．则该车间工人日均生产螺杆数的中位数是个，众数是个．

    查看试题解析

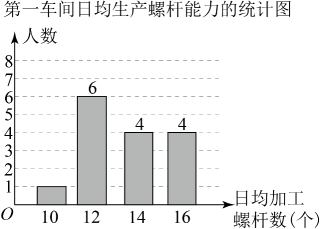  • 10. 我市体育中考有必考和选考项目，掷实心球是必考项目之一，在一次训练中，张华同学掷实心球10次的成绩依次是（单位：米）7.6，8.5，8.6，8.5，9.1，8.5，8.4，8.6，9.2，73．则张华同学撰实心球成绩的众数是 ．

    查看试题解析

  • 11. 若一组数据x，3，1，6，3的平均数和众数相等，则x的值为

    查看试题解析

  • 12. 质检部门从甲，乙两个厂家生产的同一种产品中，各抽出8件产品，对其使用寿命进行跟踪调查，结果如下（单位：年）

    甲：3，4，5，6，7，7，8，8；乙：4，6，6，6，8，9，12，13．

    已知两个厂家在广告中都称该种产品的使用寿命是6年．请根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一种特征数？

    甲： ， 乙： ．

    查看试题解析

  • 13. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

    其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

    查看试题解析

  • 14. 已知一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数为.

    查看试题解析

三、解答题

  • 15. 惠城区横沥镇陈大叔承包了甲．乙两座小山，各栽100棵荔枝树，发现成活率均为97%，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的荔枝，每棵的产量如折线统计图所示．

    (1)、直接写出甲山4棵荔枝树产量的中位数；
    (2)、分别计算甲、乙两座山荔枝样本的平均数，并判断哪座山的样本的产量高；
    (3)、用样本平均数估计甲乙两座山荔枝的产量总和．

    查看试题解析

  • 16. 某校男子足球队的年龄分布如上面的条形图所示，请找出这些队员年龄的平均数、众数、中位数，并解释它们的意义．

    查看试题解析

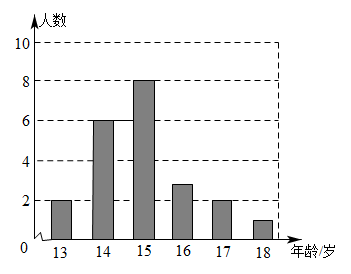  • 17. 已知一组数据：x，10，12，6的中位数与平均数相等，求x的值。

    查看试题解析

四、综合题

  • 18. 教育部办公厅在《关于进一步加强中小学生体质健康管理工作的通知》中明确要求保障学生每天校内、校外各1小时体育活动时间．某校为了解本校九年级学生每天参加体育活动的情况，随机抽取了n名学生，对某一天的体育活动时间进行了调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图．

    调查结果的频数分布表

    组别

    时间t（分钟）

    频数

    A

    30≤t<60

    5

    B

    60≤t<90

    a

    C

    90≤t<120

    b

    D

    120≤t<150

    12

    E

    t≥150

    8

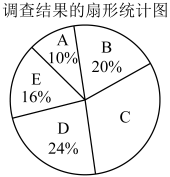
    根据上述信息，解答下列问题：

    (1)、频数分布表中的a= ， 扇形统计图中C组所在的扇形的圆心角为度；
    (2)、被抽取的n名学生这一天的体育活动时间数据的中位数在哪一组（直接写出组别即可）；
    (3)、若该校九年级共有720名学生，试估计该校九年级学生平均每天体育活动时间不低于120分钟的学生人数．

    查看试题解析

  • 19. 为了解我国2022年25个地区第一季度快递业务收入情况，收集了这25个地区第一季度快递业务收入（单位：亿元）的数据，并对数据进行了整理、描述和分析，给出如下信息．
    a．排在前5位的地区第一季度快递业务收入的数据分别为：
    5349  437.0  270.3  187.7  104.0

    b．其余20个地区第一季度快递业务收入的数据的频数分布表如下：

    快递业务收入x

    0≤x<20

    20≤x<40

    40≤x<60

    60≤x≤80

    频数

    6

    10

    1

    3

    c．第一季度快递业务收入的数据在20≤x<40这一组的是：

    20.2  20.4  22.4  24.2  26.1  26.5  28.5  34.4  39.1  39.8

    d．排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下：

     

    前5位的地区

    其余20个地区

    全部25个地区

    平均数

    306.8

    29.9

    n

    中位数

    270.3

    m

    28.5

    根据以上信息，回答下列问题：

    (1)、表中m的值为；
    (2)、在下面3个数中，与表中n的值最接近的是（填写序号）；

    ①30           ②85       ③150

    (3)、根据（2）中的数据，预计这25个地区2022年全年快递业务收入约为亿元．

    查看试题解析