2023-2024学年初中数学九年级上册 23.1 平均数与加权平均数同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 小明在爬一小山时，第一阶段的平均速度为 $2 v$ ，所用时间为t；第二阶段的平均速度为v，所用时间为 $\frac{1}{2} t$ ，则小明在爬这一小山的平均速度为（）

A、 $\frac{3}{2} v$ B、 $3 v$ C、 $\frac{5}{2} v$ D、 $\frac{5}{3} v$

查看试题解析
2. 某校举行心理剧大赛，将剧情编排、表演技巧、思想意义三个方面分别按30%，50%，20%的比例计入总分．八年级1班的各项得分如表所示，则该班的最终得分为（）
评分内容
剧情编排
表演技巧
思想意义
得分
90分
85分
95分

A、90分 B、89.5分 C、89分 D、88.5分

查看试题解析
3. 某同学使用计算器求10个数的平均数时，错误将其中一个数据12输入为22，那么由此求出的平均数比实际平均数多（）

A、1 B、10 C、2 D、 $- 1$

查看试题解析
4. 某博物馆拟招聘一名优秀志愿讲解员，其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分，综合成绩中笔试占 $30 %$ ，试讲占 $50 %$ ，面试占 $20 %$ ，则该名志愿者的综合成绩为（）

A、94分 B、92.4分 C、92分 D、90.5分

查看试题解析
5. 已知一组数据2，3， $x$ 的平均数是2，则这组数据中的 $x$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析
7. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
8.
为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m³），绘制了统计图．如图所示，下面四个推断（　　）
①年用水量不超过180m³的该市居民家庭按第一档水价交费；
②年用水量超过240m³的该市居民家庭按第三档水价交费；
③该市居民家庭年用水量的中位数在150﹣180之间；
④该市居民家庭年用水量的平均数不超过180．

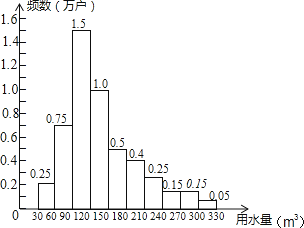A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

9. 小张到某建筑公司打工，公司承诺：正常上班的工资为150元/天，不能正常上班的工资为50元/天．如果某月（30天）正常上班的天数占80%，其余天数不能正常上班，则当月小张的日平均工资为元．

查看试题解析

10. 学校要从两位同学中选拔1人担任运动会志愿者，选拔项目及两人得分如下表所示，若将普通话、体育知识和旅游知识依次按4：3：3记分．则最终胜出的同学是．

	普通话	体育知识	旅游知识
小聪	80	90	72
小慧	90	80	70

查看试题解析

11. 两台A、B型号的大米自动封装机包装的质量为

50 k m

的袋食品中各封装了10袋大米，测得其实际质量如下表（单位：

k m

）：

A	$50.1$	$\begin{array}{l} 50.6 \end{array}$	$\begin{array}{l} 50.8 \end{array}$	$49.7$	$\begin{array}{l} 50.8 \end{array}$	$49.6$	$50.5$	$50.3$	$\begin{array}{l} 49.5 \end{array}$	$\begin{array}{l} 49.9 \end{array}$
B	$50.5$	$\begin{array}{l} 50.2 \end{array}$	$\begin{array}{l} 49.8 \end{array}$	$50.1$	$\begin{array}{l} 49.9 \end{array}$	$50.3$	$\begin{array}{l} 49.8 \end{array}$	$\begin{array}{l} 50.2 \end{array}$	$50.1$	$\begin{array}{l} 49.9 \end{array}$

由上表可以判断型号自动封装机性能更好．

查看试题解析

12. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析
13. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析

三、计算题

14. 已知两个有理数：－9和5．

(1)、计算： $\frac{(- 9) + 5}{2}$ ；

(2)、若再添一个负整数 $m$ ，且－9，5与 $m$ 这三个数的平均数仍小于m，求m的值．

查看试题解析

四、解答题

15. 某学校评选先进班集体，从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分，各项满分均为100分，按比例计算综合得分，各项所占比例如表所示：

项目学习卫生纪律活动参与

所占比例 40% 25% 25% 10%

八年级（1）班这四项得分依次为95分，90分，88分，80分，若学校规定班级四项综合得分超过90分的将会获得先进班集体，请你通过计算说明该班是否会获得先进班集体？

查看试题解析
16. 2022年5月30日是第六个全国科技工作者日，主题为“创新争先，自立自强”．为了庆祝第六个全国科技工作者日，学校举办科技知识竞赛活动，竞赛内容分“航天技术”，“生物技术”，“能源技术”，“其它技术领域”四个项目，下表是小亮和小明的各项成绩：（百分制）

航天技术
生物技术
能源技术
其它技术领域
小亮
85
90
95
90
小明
100
90
80
90
若“航天技术”，“生物技术”，“能源技术”，“其它技术领域”四个项目按 $4 ： 3 ： 2 ： 1$ 确定综合成绩，则小亮和小明谁的综合成绩高？请通过计算说明理由．

查看试题解析

五、综合题

17. 已知5个数a₁ ， a₂ ， a₃ ， a₄ ， a₅的平均数为m，则

(1)、a₁ ， a₂ ， a₃ ， 0，a₄ ， a₅ ，这6个数的平均数为；

(2)、2a₁ ， 2a₂ ， 2a₃ ， 2a_4，2a₅这5个数的平均数为；

(3)、若5个数b₁ ， b₂ ， b₃ ， b₄ ， b₅的平均数为n，则2a₁+b₁ ， 2a₂+b₂ ， 2a₃+b₃ ， 2a₄+b₄ ， 2a₅+b₅这5个数的平均数为。

查看试题解析
18. 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如右表．

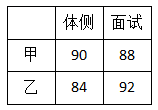(1)、当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？

(2)、当体侧成绩权重为 $a$ ，面试和体侧各有权重，并且权总和为10，请问当 $a$ 取什么范围，乙成绩比甲高？

查看试题解析

评分内容	剧情编排	表演技巧	思想意义
得分	90分	85分	95分

项目	学习	卫生	纪律	活动参与
所占比例	40%	25%	25%	10%

	航天技术	生物技术	能源技术	其它技术领域
小亮	85	90	95	90
小明	100	90	80	90

2023-2024学年初中数学九年级上册 23.1 平均数与加权平均数 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023-2024学年初中数学九年级上册 23.1 平均数与加权平均数同步分层训练培优卷(冀教版)