2023-2024学年初中数学九年级上册 23.1 平均数与加权平均数同步分层训练基础卷(冀教版)

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题

1. 一组数据x、0、1、－2、3的平均数是1，则x的值是（）

A、3 B、1 C、2.5 D、0

查看试题解析
2. 某校人工智能科普社团有12名成员，成员的年龄情况统计如下：
年龄（岁）
12
13
14
15
16
人数（人）
1
4
3
2
2
则这12名成员的平均年龄是（）

A、13岁 B、14岁 C、15岁 D、16岁

查看试题解析
3. 某校在计算学生的数学总评成绩时，规定期中考试成绩占40%，期末考试成绩占60%，林琳同学的期中数学考试成绩为 $86$ 分，期末数学考试成绩为94分，那么他的数学总评成绩是（）

A、86分 B、88分 C、90分 D、90.8分

查看试题解析
4. 已知一组数据 $x_{1} ， x_{2} ， x_{3}$ 的平均数为3，则数据 $x_{1} + 2 ， x_{2} + 2 ， x_{3} + 2$ 的平均数是（）

A、3 B、5 C、6 D、7

查看试题解析
5. 希望中学规定学生的学期体育成绩满分为 $100$ ，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%若小强的三项成绩 $($ 百分制 $)$ 依次是95，90，91则小强这学期的体育成绩是（）

A、92 B、91.5 C、91 D、90

查看试题解析
6. 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分（　　）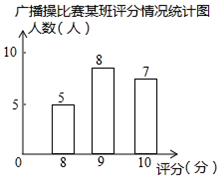

A、9 B、6.67 C、9.1 D、6.74

查看试题解析
7. 如果数据2，3，x ， 4的平均数是3，那么x等于（）．

A、2 B、3 C、3.5 D、4

查看试题解析
8. 小明随机抽查了九年级（2）班9位同学一周写数学作业的时间，分别为6，4，6，5，6，7，6，6，8（单位：h）.则估计本班大多数同学一周写数学作业的时间约为（）

A、4h B、5h C、6h D、7h

查看试题解析

二、填空题

9. 某招聘考试分笔试和面试两种．其中笔试按80%、面试按20%计算加权平均数作为总成绩．小明笔试成绩为90分面试成绩为85分，那么小明的总成绩为分．

查看试题解析
10. 有一组数：x₁ ， x₂ ， x₃…x₁₀ ，若这组数的前4个数的平均数为12，后6个数的平均数为15，则这组数的平均数为.

查看试题解析
11. 如图为某学校学生年龄分布情况扇形统计图，根据统计图，解决下列问题：

(1)、m=；

(2)、该学校学生的平均年龄为岁．

查看试题解析
12. 若 $a$ 、 $b$ 、 $c$ 的平均数为 $7$ ，则 $a + 1$ 、 $b + 2$ 、 $c + 3$ 的平均数为．

查看试题解析

13. 某校欲招聘一名数学教师，学校对甲乙丙三位候选人进行三项能力测试，各项成绩满分均为100分，根据结果择优录用，三位候选人测试成绩如表：

测试项目	成绩
测试项目	甲	乙	丙
教学能力	77	73	73
科研能力	70	71	65
组织能力	64	72	84

根据实际需要学校将三项能力测试得分按6：2：2的比例确定每人的成绩，将被录用的是

查看试题解析

三、解答题

14. 某公司招聘一名部门经理，对A、B、C三位候选人进行了三项测试，成绩如下（单位：分）：

候选人	语言表达	微机操作	商品知识
A	60	80	70
B	50	70	80
C	60	80	65

如果语言表达、微机操作和商品知识的成绩按3∶3∶4计算，那么谁将会被录取？