2023年九年级上册数学人教版单元分层测试第二十二章二次函数 A卷

试卷更新日期：2023-08-12 类型：单元试卷

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，二次函数 $y = 2 {(x - 1)}^{2} + 3$ 的顶点坐标是（）

A、 $(1 ， 3)$ B、 $(1 ， - 3)$ C、 $(- 1 ， 3)$ D、 $(- 1 ， - 3)$

查看试题解析
2. 关于二次函数 $y = - (x + 2)^{2} - 3$ 的图象，下列说法错误的是（）

A、开口向下 B、对称轴是直线 $x = 2$ C、与x轴没有交点 D、当 $x > - 1$ 时，y随x的增大而减小

查看试题解析
3. 已知实心球运动的高度 $y (m)$ 与水平距离 $x (m)$ 之间的函数关系是 $y = - {(x - 1)}^{2} + 4$ ，则该同学此次投掷实心球的成绩是（）

A、 $2 m$ B、 $3 m$ C、 $3.5 m$ D、 $4 m$

查看试题解析
4. 关于x的二次函数 $y = - x^{2} + (a - 2) x - 3$ 在y轴右侧y随x的增大而减小，则a的范围为（）

A、 $a < 2$ B、 $a \leq 2$ C、 $a > 2$ D、 $a = 2$

查看试题解析
5. 将抛物线 $y = x^{2}$ 向上平移3个单位长度得到的抛物线是（）

A、 $y = x^{2} + 3$ B、 $y = x^{2} - 3$ C、 $y = {(x + 3)}^{2}$ D、 $y = {(x - 3)}^{2}$

查看试题解析
6. 小兰画了一个函数 $y = x^{2} + a x + b$ 的图象如图，关于 $x$ 的方程 $x^{2} + a x + b = 0$ 的解是（）

A、无解 B、 $x = 1$ C、 $x = - 4$ D、 $x = - 1$ 或 $x = 4$

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c (a < 0)$ 的图象与x轴的一个交点坐标为 $(- 1 ， 0)$ ，对称轴为直线 $x = 1$ ，下列论中：① $a - b + c = 0$ ；②若点 $(- 3 ， y_{1}) ， (2 ， y_{2}) ， (4 ， y_{3})$ 均在该二次函数图象上，则 $y_{1} < y_{2} < y_{3}$ ；③若m为任意实数，则 $a m^{2} + b m + c \leq - 4 a$ ；④方程 $a x^{2} + b x + c + 1 = 0$ 的两实数根为 $x_{1} ， x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $x_{1} < - 1 ， x_{2} > 3$ ．正确结论的序号为（）

A、①②③ B、①③④ C、②③④ D、①④

查看试题解析
8. 抛物线 $y = a x^{2} + b x + c$ 的顶点为 $D (- 1 ， 2)$ ，与x轴的一个交点A在点 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，其部分图象如图，则以下结论：① $b^{2} - 4 a c < 0$ ； ②当 $x > - 1$ 时，y随x增大而减小；③ $a + b + c < 0$ ； ④若方程 $a x^{2} + b x + c - m = 0$ 没有实数根，则 $m > 2$ ；⑤ $3 a + c > 0$ ，其中正确结论的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

9. 抛物线 $y = x^{2} + b x + c$ 的对称轴是直线 $x = - 1$ ，则 $b =$ ．

查看试题解析
10. 已知二次函数 $y = - a x^{2} + 2 a x + 3 (a > 0)$ ，若点 $P (m ， 3)$ 在该函数的图象上，且 $m \neq 0$ ，则 $m$ 的值为.

查看试题解析
11. 如图，二次函数y＝ax²+bx+c（a≠0）图象经过点A（-1，-2），对称轴为直线x＝1，则9a+3b+c的值是．

查看试题解析
12. 如图，在平面直角坐标中，抛物线 $y = a x^{2} + b x (a > 0)$ 和直线 $y = k x (k > 0)$ 交于点 $O$ 和点 $A$ ，则不等式 $a x^{2} + b x < k x$ 的解集为．

查看试题解析
13. 如果点 $M (- 2 ， y_{1})$ ， $N (- 1 ， y_{2})$ 在二次函数 $y = - x^{2} + 2 x$ 的图象上，则 $y_{1}$ $y_{2}$ （填“＞”、“＜”或“＝”）

查看试题解析
14. 如图，王叔叔想用长为 $60 m$ 的栅栏，再借助房屋的外墙围成一个矩形羊圈 $A B C D$ ，已知房屋外墙足够长，当矩形 $A B C D$ 的边 $A B =$ $m$ 时，羊圈的面积最大．

查看试题解析
15. $2023$ 年5月8日， $C 919$ 商业首航完成——中国民商业运营国产大飞机正式起步． $12$ 时 $31$ 分航班抵达北京首都机场，穿过隆重的“水门礼”（寓意“接风洗尘”、是国际民航中高级别的礼仪）．如图①，在一次“水门礼”的预演中，两辆消防车面向飞机喷射水柱，喷射的两条水柱近似看作形状相同的抛物线的一部分．如图②，当两辆消防车喷水口A、B的水平距离为 $80$ 米时，两条水柱在物线的顶点H处相遇，此时相遇点H距地面 $20$ 米，喷水口A、B距地面均为4米．若两辆消防车同时后退 $10$ 米，两条水柱的形状及喷水口 $A^{'}$ 、 $B^{'}$ 到地面的距离均保持不变，则此时两条水柱相遇点 $H^{'}$ 距地面米．

查看试题解析

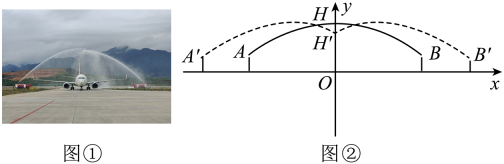
三、解答题

16. 城建部门计划修建一条喷泉步行通道．图1是项目俯视示意图．步行通道的一侧是一排垂直于路面的柱形喷水装置，另一侧是方形水池．图2是主视示意图．喷水装置 $O A$ 的高度是2米，水流从喷头A处喷出后呈抛物线路径落入水池内，当水流在与喷头水平距离为2米时达到最高点B，此时距路面的最大高度为3.6米．为避免溅起的水雾影响通道上的行人，计划安装一个透明的倾斜防水罩，防水罩的一端固定在喷水装置上的点 $M$ 处，另一端与路面的垂直高度 $N C$ 为1.8米，且与喷泉水流的水平距离 $N D$ 为0.3米．点 $C$ 到水池外壁的水平距离 $C E = 0.6$ 米，求步行通道的宽 $O E$ ．（结果精确到0.1米）参考数据： $\sqrt{2} \approx 1.41$

查看试题解析

17. 【问题背景】

“刻漏”是我国古代的一种利用水流计时的工具．综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀（控制水的流速大小）的软管制作简易计时装置．

【实验操作】

综合实践小组设计了如下的实验：先在甲容器里加满水，此时水面高度为30cm，开始放水后每隔10min观察一次甲容器中的水面高度，获得的数据如下表：

流水时间t/min	0	10	20	30	40
水面高度h/cm（观察值）	30	29	28.1	27	25.8

任务1 分别计算表中每隔10min水面高度观察值的变化量．

【建立模型】

小组讨论发现：“ $t = 0$ ， $h = 30$ ”是初始状态下的准确数据，水面高度值的变化不均匀，但可以用一次函数近似地刻画水面高度h与流水时间t的关系．

任务2 利用 $t = 0$ 时， $h = 30$ ； $t = 10$ 时， $h = 29$ 这两组数据求水面高度h与流水时间t的函数解析式．

【反思优化】

经检验，发现有两组表中观察值不满足任务2中求出的函数解析式，存在偏差．小组决定优化函数解析式，减少偏差．通过查阅资料后知道：t为表中数据时，根据解析式求出所对应的函数值，计算这些函数值与对应h的观察值之差的平方和，记为w；w越小，偏差越小．

任务3 ⑴计算任务2得到的函数解析式的w值．

⑵请确定经过 $(0 ， 30)$ 的一次函数解析式，使得w的值最小．

【设计刻度】

得到优化的函数解析式后，综合实践小组决定在甲容器外壁设计刻度，通过刻度直接读取时间．

任务4 请你简要写出时间刻度的设计方案．

查看试题解析

18. 根据以下素材，探索完成任务

如何设计拱桥上救生圈的悬挂方案?
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示．某时测得水面宽 $20 m$ ，拱顶离水面最大距离为10m，抛物线拱形最高点与x轴的距离为5m．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，救生圈悬挂点为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m．为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）
问题解决
任务1	确定桥拱形状	根据图2，求抛物线的函数表达式．
任务2	拟定设计方案	求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
任务3	探究救生绳长度	当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）