2023年八年级上册数学人教版单元分层测试 第十一章 三角形 B卷
试卷更新日期:2023-08-12 类型:单元试卷
一、选择题
-
1. 下列长度的三条线段能构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,2. 如图,在直角三角形中, , , , 则的度数为( )
 A、 B、 C、 D、3. 如图,是的中线,点E为的中点,连接 , 若的面积为 , 则的面积为( )
A、 B、 C、 D、3. 如图,是的中线,点E为的中点,连接 , 若的面积为 , 则的面积为( ) A、3 B、5 C、4 D、64. 某市为了方便市民绿色出行,推出了共享单车服务,图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中 , 都与地面l平行, , , 当为( )度时,与平行.
A、3 B、5 C、4 D、64. 某市为了方便市民绿色出行,推出了共享单车服务,图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中 , 都与地面l平行, , , 当为( )度时,与平行. A、54 B、64 C、74 D、1145. 下列正多边形的组合中,能够铺满地面的是( )A、正八边形和正三角形 B、正八边形和正方形 C、正八边形和正五角形 D、正六边形和正方形6. 若将一副三角板按如图的方式放置,若 , 则的度数为( )
A、54 B、64 C、74 D、1145. 下列正多边形的组合中,能够铺满地面的是( )A、正八边形和正三角形 B、正八边形和正方形 C、正八边形和正五角形 D、正六边形和正方形6. 若将一副三角板按如图的方式放置,若 , 则的度数为( ) A、 B、 C、 D、7. 如图所示,已知直线AB、CD被直线AC所截,是平面内任意一点(点不在直线AB、CD、AC上),设∠BAE , ∠DCE=与均小于 , 在下列各式中:①;②;③;④ , 可能为大小的是( )
A、 B、 C、 D、7. 如图所示,已知直线AB、CD被直线AC所截,是平面内任意一点(点不在直线AB、CD、AC上),设∠BAE , ∠DCE=与均小于 , 在下列各式中:①;②;③;④ , 可能为大小的是( ) A、①②③ B、②③④ C、①②④ D、①②③④8. 如图, , AE⊥EF,E在BC上,过E作EC⊥DC,EG平分∠FEC,ED平分∠AEC.若∠EAD+∠BAD=180°,∠EDA=3∠CEG,则下列结论:①∠EAB=2∠FEG;②∠AED=45°+∠GEF;③∠EAD=135°-4∠GEC;④∠EAB=15°,其中正确的是( )
A、①②③ B、②③④ C、①②④ D、①②③④8. 如图, , AE⊥EF,E在BC上,过E作EC⊥DC,EG平分∠FEC,ED平分∠AEC.若∠EAD+∠BAD=180°,∠EDA=3∠CEG,则下列结论:①∠EAB=2∠FEG;②∠AED=45°+∠GEF;③∠EAD=135°-4∠GEC;④∠EAB=15°,其中正确的是( ) A、①②③④ B、①③④ C、①②④ D、①②③9. 正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为 . 现有格点 , 那么,在网格图中找出格点 , 使以和格点为顶点的三角形的面积为1.这样的点可找到的个数为( )
A、①②③④ B、①③④ C、①②④ D、①②③9. 正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为 . 现有格点 , 那么,在网格图中找出格点 , 使以和格点为顶点的三角形的面积为1.这样的点可找到的个数为( ) A、4 B、5 C、6 D、710. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )
A、4 B、5 C、6 D、710. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )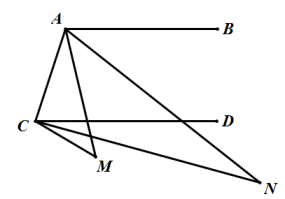 A、21.5° B、21° C、22.5° D、22°
A、21.5° B、21° C、22.5° D、22°二、填空题
-
11. 如图,在中,是边上的中线,若 , , 则点D到的距离为 .
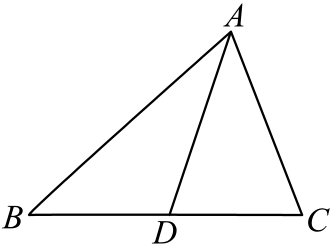 12. 如图,在中, , 分别是边和上的两点,连接 , 若 , 则的度数为(用含的式子表示).
12. 如图,在中, , 分别是边和上的两点,连接 , 若 , 则的度数为(用含的式子表示). 13. 如图, , 分别是的内角平分线和外角平分线, , 分别是的内角平分线和外角平分线, , 分别是的内角平分线和外角平分线……以此类推,若 , 则 .
13. 如图, , 分别是的内角平分线和外角平分线, , 分别是的内角平分线和外角平分线, , 分别是的内角平分线和外角平分线……以此类推,若 , 则 . 14. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .
14. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .

三、解答题
-
15. 探究归纳题:
 (1)、试验分析:
(1)、试验分析:如图1,经过A点可以作条对角线;同样,经过B点可以作条;经过C点可以作条;经过D点可以作条对角线.
通过以上分析和总结,图1共有条对角线.
(2)、拓展延伸:运用(1)的分析方法,可得:
图2共有条对角线;
图3共有条对角线;
(3)、探索归纳:对于n边形(n>3),共有条对角线.(用含n的式子表示)
(4)、特例验证:十边形有条对角线.
16. 小明在学习过程中,对教材中的一个有趣问题做如下探究: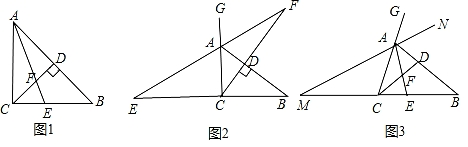
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
17. 用两种方法证明“三角形的外角和等于360°”;如图,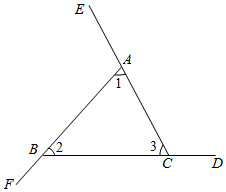
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角
∴__▲_.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
∵_▲_.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2
四、综合题
-
18. 如图
 (1)、【问题】如图①,在△ABC中,∠A=74°,DB平分∠ABC,DC平分∠ACB.求∠D的度数,对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
(1)、【问题】如图①,在△ABC中,∠A=74°,DB平分∠ABC,DC平分∠ACB.求∠D的度数,对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).解:∵∠ABC+∠ACB+∠A=180°(三角形内角和180° ).
∴∠ABC+∠ACB= ▲ (等式性质).
∵∠A=74° (已知),
∴∠ABC+∠ACB= ▲ (等量代换).
∵DB平分∠ABC(已知),
∴∠DBC=∠ABC(角平分线的定义).
同理,∠DCB= ▲ ;
∴(∠ABC+∠ACB)= ▲ (等式性质).
∵∠DBC+∠DCB+∠D=180°,
∴∠D=180°-(∠DBC+∠DCB)= ▲ (等式性质).
(2)、【拓展】如图②,在△ABC中,∠A=β,DB平分∠ABC,DC平分∠ACB.则∠D=( ).
(3)、【应用】如图③,在△ABC中,DB平分∠ABC,DC平分∠ACB,EB平分∠DBC,EC平分∠DCB.若∠E=146°,则∠A= .19.[课题学习]:
平行线的“等角转化”功能.
 (1)、[阅读理解]:
(1)、[阅读理解]:如图1,已知点是外一点,连接 , , 求的度数.
阅读并补充下面推理过程.
解:过点作 , 所以 ,
又因为
所以
(2)、[方法运用]:如图2,已知 , 求的度数.
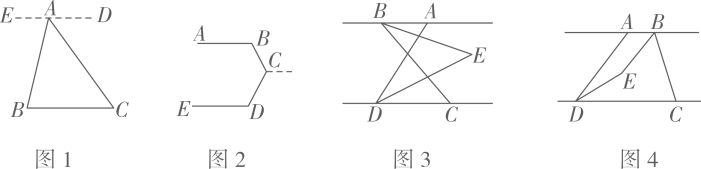
(3)、[深化拓展]:已知 , 点在的右侧, , 平分 , 平分 , , 所在的直线交于点 , 点在与两条平行线之间.
①如图3,若 , 则°
②如图4,点在点的右侧,若 , 则°(用含的代数式表示)