2023年浙教版数学八年级上册1.3 证明同步测试（提高版）

试卷更新日期：2023-08-12 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共15分）

1. 如图， $∠ D C A = 60 °$ ，要证 $A B / / C D$ ，需要的条件是（）

A、 $∠ E A D = 60 °$ B、 $∠ B = 60 °$ C、 $∠ B C D = 120 °$ D、 $∠ E A C = 120 °$

查看试题解析
2. △ABC中，∠A＝∠B+∠C，则对△ABC的形状判断正确的是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
3. 如图，以下条件不能判断 $A B ∥ C D$ 的是（）

A、 $∠ 2 = ∠ 3$ B、 $∠ 1 = ∠ 2$ C、 $∠ 4 = ∠ 1 + ∠ 3$ D、 $∠ A B C + ∠ B C D = 180 °$

查看试题解析
4. 如图，下列判断正确的是（）

A、∠1和∠2是同旁内角 B、∠3和∠7是同位角 C、∠5和∠6是同旁内角 D、∠4和∠3是同位角

查看试题解析
5. 如图，在四边形ABCD中，连接AC，下列判断正确的是（）

A、若 $∠ 1 = ∠ 2$ ，则 $A D ∥ B C$ B、若 $A B ∥ C D$ ，则 $∠ 3 = ∠ 4$ C、若 $∠ B A D + ∠ B C D = 180 °$ ，则 $A D ∥ B C$ D、若 $∠ B A D = ∠ D C B$ ， $∠ B = ∠ D$ ，则 $A B ∥ C D$

查看试题解析

二、填空题（每空3分，共21分）

6. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 $A = a^{2} + a$ ，请结合你所学知识，判断下列说法：①当 $a = - 2$ 时， $A = 2$ ；②无论a取任何实数，不等式 $A + \frac{1}{4} \geq 0$ 恒成立；③若 $A - 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} = 4$ ；正确的有.

查看试题解析
7.
如图所示，在△ABC中，∠1=∠2，G是AD的中点，延长BG交AC于点E，F为AB上一点，CF⊥AD交AD于点H．①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH为△ACD的边AD上的高；④AH是△ACF的角平分线和高线，其中判断正确的有.

查看试题解析
8. 如图，直线a，b都与直线c相交，下列命题中，能判断a∥b的条件是（把你认为正确的序号填在横线上）。
1 、∠1=∠2 2、 ∠3=∠6 3、 ∠1=∠8 4 、∠5+∠8=180°

查看试题解析
9. 将一块三角板ABC（∠BAC＝90°，∠ABC＝30°）按如图方式放置，使A，B两点分别落在直线m，n上，对于给出的四个条件：①∠1＝25.5°，∠2＝55.5°；②∠1+∠2＝90°；③∠2＝2∠1；④∠ACB＝∠1+∠3；⑤∠ABC＝∠2﹣∠1．能判断直线m $/ /$ n的有．（填序号）

查看试题解析
10. 判断： ${\begin{cases} x = - 2 \\ y = 2 \end{cases}$ (填“是”或“不是”)方程组 ${\begin{cases} 3 x + 4 y = 2 \\ 2 x - y = 5 \end{cases}$ 的解。

查看试题解析
11. 一家电脑生产厂家在某城市三个经销本厂产品的大商场调查，产品的销量占这三个大商场同类产品销量的40%，由此在广告中宣传，他们的产品在国内同类产品的销售量占40%．请你根据所学的统计知识，判断该宣传中的数据是否可靠：，理由是．

查看试题解析

三、解答题（共18题，共114分）

12. 如图，已知点A、C分别在∠GBE的边BG、BE上，且AB=AC，AD∥BE，∠GBE的平分线与AD交于点D，连接CD．
证：①AB=AD；

②CD平分∠ACE．

查看试题解析
13. 如图，点D是等边 $△ A B C$ 中边 $A C$ 上的任意一点，且 $△ B D E$ 也是等边三角形，那么 $A E$ 与 $B C$ 平行吗？请说明理由．

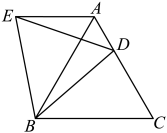
解：因为 $△ A B C$ 是等边三角形（已知），
所以 $B C = B A$ （等边三角形各边相等），
      $∠ C = ∠ C A B = ∠ A B C = 60 °$ （等边三角形每个内角都是 $60 °$ ）；
因为 $△ B D E$ 是等边三角形（已知），
所以 $E B = D B$ （  ），
      $∠ E B D = 60 °$ （  ）；
所以 $∠ A B C = ∠ E B D$ （  ），
所以 $∠ A B C - ∠$        ▲   $= ∠ E B D -$        ▲  （等量减等量），
即∠       ▲  =∠       ▲  ；
在 $△ A B E$ 和 $△ C B D$ 中
      ${\begin{array}{l} B A = B C (已证) ， \\ ∠ ▲ = ∠ ▲ (已证) ， \\ E B = D B (已证) ， \end{array}$
所以 $△ A B E ≌ △ C B D$ （  ）．
所以 $∠ E A B = ∠$        ▲   $= 60 °$ （  ），
所以 $∠ E A B + ∠ B A C = 60 ° + 60 ° = 120 °$ ，
所以 $∠ E A C + ∠ C = 120 ° + 60 ° = 180 °$ ，
所以 $A E ∥ B C$ （  ）．

查看试题解析
14. 在 $△ A B C$ 中，如果 $∠ A = 2 ∠ B = 3 ∠ C$ ，那么你能判断 $△ A B C$ 是什么三角形吗？

查看试题解析
15. 如图，BA平分∠EBC，CD平分∠ACF，且AB∥CD．试判断AC与BE的位置关系，并说明理由．

查看试题解析
16. 如图，已知A，B，C三点在同一条直线上，且AD∥BE，∠3=∠1，试判断BD与CE的位置关系，并说明理由.

查看试题解析
17. 如果 $Δ A B C$ 的三边长 $a ， b ， c$ 满足等式 $a^{2} + b^{2} + c^{2} - a b - b c - c a = 0$ ，试判断此 $Δ A B C$ 的形状并写出你的判断依据．

查看试题解析
18. 如图，已知 $A B ∥ C D$ ，试判断 $∠ B$ ， $∠ B E D$ 和 $∠ D$ 之间的关系，并说明理由．

查看试题解析
19. 如图∠1+∠2＝180°， $∠ A E F = ∠ H L N$ ，判断图中有哪些直线平行？并给予说理．

查看试题解析
20. 小红与小亮两位同学计算-3²-6×（ $\frac{1}{2} - \frac{1}{3}$ ）的过程如图：

请判断他们的解法是否正确（在相应的方框内打“√”或“×”），并写出你的解答过程．

查看试题解析
21. 计算 $6 \div (- \frac{1}{2} + \frac{1}{3})$ 时，李明同学的计算过程如下：
原式＝6÷ $(- \frac{1}{2}) + 6 \div \frac{1}{3}$ ＝－12＋18＝6.

请你判断李明的计算过程是否正确，若不正确，请你写出正确的计算过程，另用正确方法计算 $(\frac{1}{2} - \frac{1}{6} + \frac{1}{9}) \div (- \frac{1}{36}) + 36 \div (\frac{1}{2} - \frac{1}{6} + \frac{1}{9})$ 的值.

查看试题解析
22. 若△ABC的三边a、b、c满足|a﹣15|+（b﹣8）²+ $\sqrt{c - 17}$ =0，试判断△ABC的形状，并说明理由．

查看试题解析
23. 如图，将连续的偶数2，4，6，8，10，…排成一数阵，有一个能够在数阵中上下左右平移的T字架，它可以框出数阵中的五个数．试判断这五个数的和能否为426？若能，请求出这五个数；若不能，请说明理由．

查看试题解析
24. 如果A=5x²+4x﹣1，B=﹣x²﹣3x﹣3，C=8﹣7x﹣6x² ，小聪在计算A﹣B+C的值后判断A﹣B+C的值与x无关，请你说明小聪的判断是否正确，并说明理由．

查看试题解析
25. 将一副三角板按如图方式进行摆放，请判断∠1，∠2是否互补，并说明理由．

查看试题解析
26. 要比较a与b的大小,可以先求a与b的差,再看这个差是正数、负数还是零.由此可见,要判断两个式子值的大小,只要考虑它们的差就可以了.
已知A=16a²+a+15 , B=4a²+ $\frac{1}{2}$ a+7 , C=a²+ $\frac{1}{3}$ a+4.

(1)、请你按照上述文字提供的信息:(1)试比较A与2B的大小;

(2)、试比较2B与3C的大小.

查看试题解析
27.
填写推证理由：已知：如图①，AB和CD相交于点O，∠A=∠AOC，∠B=∠BOD． ${\begin{array}{l} x + 4 y = 46 \\ 2 x + 3 y = 57 \end{array}$ 求证：AC $∥$ BD．

(1)、证明：∵ ∠A=∠AOC，∠B=∠BOD，

又 ∠AOC=∠BOD（   ），

∴ ∠A=∠B．

∴AC $∥$ BD（   ）．

(2)、如图②，直线AB、CD相交于点O，OE⊥AB．若∠AOC︰∠AOE=2︰3，求∠DOE的度数．

查看试题解析
28. 综合与实践
问题情境：
数学课上，老师让同学们以“三角板与平行线”为主题开展数学活动．如图1，已知l₁∥l₂ ，直角三角板ABC中，∠B＝90°，将其顶点A放在直线l₂上，并使边AB⊥直线l₁于点D，AC与l₁相交于点H．老师提出问题：试判断边BC与直线l₁的位置关系并说明理由．

(1)、请解答老师提出的问题：

(2)、如图2，将图1中三角板ABC的直角顶点B放在平行线之间，两直角边AB，CB分别与l₁_，l₂相交于点P，Q，得到∠1和∠2，试探究∠1与∠2的数量关系并说明理由．
下面是小亮不完整的解答过程和解题反思，请你补充完整：
解：∠1＋∠2＝90°．过点B作直线BN∥l₁ ，如图：
∵l₁∥l₂（已知）
∴BN∥l₂（                ）
∴∠1=  ▲  ∠2=  ▲  （                ）
∵∠  ▲  +∠   ▲  =∠ABC，∠ABC=90°
∴∠1＋∠2＝90°
解题反思：在图中“过点B作直线BN∥l₁”的作用是  ▲

(3)、受小亮启发，同学们续探究下列问题．
请从下列A，B两题中任选一题作答．我选择  ▲
A．在图2中作线段PO和QO，使它们分别平分∠1和∠2的对顶角，如图3．直接写出∠POQ的度数．
B．在图2中∠ABC内部作射线BE，过点B作射线BF⊥BE交直线L₂于点M，得到∠3，如图4．直接写出∠1，∠3与∠EBC的数量关系．

查看试题解析
29. 小明完成暑假作业后在家复习，他看到七下课本12页例4：“如图1﹣13，AP平分∠BAC，CP平分∠ACD，∠1+∠2＝90°.判断AB，CD是否平行，并说明理由.”，试着“玩”起数学来：

(1)、【基础巩固】
条件和结论互换，改成了：“如图1﹣13，AP平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2＝90°.”小明认为这个结论正确.你赞同他的想法吗？请说明理由.

(2)、【尝试探究】
小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2＝90°”这个结论不成立.请帮小明完成探究：
如图1，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2是CP与CD的夹角，

①若∠2＝22°，求∠1的度数；

②试说明：2∠1﹣∠2＝90°.

(3)、【拓展提高】
如图2，若AB∥CD，AP⊥AC，CP平分∠ACD，请直接写出∠1与∠2的等量关系.

查看试题解析