2023年浙教版数学八年级上册1.3 证明 同步测试(培优版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 在下列生活实例中,数学依据不正确的是( )A、在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线; B、在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点之间线段最短; C、从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,大大节约了路程,依据的是两点之间线段最短; D、体育课上,体育老师测量跳远距离的时候,测的是落脚脚跟到起跳线的距离,依据的是垂线段最短.2. 如图,用剪刀沿图中虚线将一个正方形图片减掉一部分,发现剩下部分的周长比原正方片的周长要小,能解释这一现象的数学知识是( )
 A、垂线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短3. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )
A、垂线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短3. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )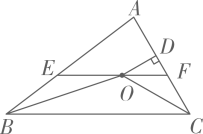 A、1个 B、2个 C、3个 D、4个4. 如图,将两张长为 , 宽为的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为和若知道下列条件,仍不能求值的是( )
A、1个 B、2个 C、3个 D、4个4. 如图,将两张长为 , 宽为的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为和若知道下列条件,仍不能求值的是( ) A、长方形纸片长和宽的差 B、长方形纸片的周长和面积 C、①和②的面积差 D、长方形纸片和①的面积差5. 如图,ABCD,PG平分∠EPF,∠A+∠AHP=180°,下列结论:①CDPH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP-∠FPG=180°;其中正确结论是( )
A、长方形纸片长和宽的差 B、长方形纸片的周长和面积 C、①和②的面积差 D、长方形纸片和①的面积差5. 如图,ABCD,PG平分∠EPF,∠A+∠AHP=180°,下列结论:①CDPH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP-∠FPG=180°;其中正确结论是( ) A、①②③④ B、①②④ C、①③④ D、①②6. 如图a∥b,与相交,与相交,下列说法:
A、①②③④ B、①②④ C、①③④ D、①②6. 如图a∥b,与相交,与相交,下列说法:①若 , 则;
②若 , 则c∥d;
③;
④ ,
正确的有( )
 A、①③④ B、①②③ C、①②④ D、②③7. 如图,C、D是线段AB上两点,M、N分别是线段AD,BC的中点,下列结论:
A、①③④ B、①②③ C、①②④ D、②③7. 如图,C、D是线段AB上两点,M、N分别是线段AD,BC的中点,下列结论:①若AD=BM,则AB=3BD;②AC=BD,则AM=BN;③AC﹣BD=2(MC﹣DN);④2MN=AB﹣CD.
其中正确的结论是( )
 A、①②③ B、③④ C、①②④ D、①②③④8. 如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12.其中正确结论的个数是( )
A、①②③ B、③④ C、①②④ D、①②③④8. 如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12.其中正确结论的个数是( )
 A、1 B、2 C、3 D、49. 若 , 为实数且满足 , , 设 , , 有以下2个结论:若 , 则;若 , 则下列判断正确的是( )A、①对②错 B、①错②对 C、①②都错 D、①②都对10. 在以下三个图形中,根据尺规作图的痕迹,不能判断射线AD平分∠BAC的是( )
A、1 B、2 C、3 D、49. 若 , 为实数且满足 , , 设 , , 有以下2个结论:若 , 则;若 , 则下列判断正确的是( )A、①对②错 B、①错②对 C、①②都错 D、①②都对10. 在以下三个图形中,根据尺规作图的痕迹,不能判断射线AD平分∠BAC的是( ) A、图2 B、图1与图2 C、图1与图3 D、图2与图3
A、图2 B、图1与图2 C、图1与图3 D、图2与图3二、填空题(每空4分,共20分)
-
11. 在数轴上和有理数a,b,c对应的点的位置如图所示,有下面四个结论:

① , ② , ③ , ④ , ⑤其中,正确的结论有(填序号).
12. 若 ,且 ,以下结论:① , ;
②关于x的方程 的解为 ;
③
④ 的值为0或2;
⑤在数轴上点A.B.C表示数a、b、c,若 ,则线段AB与线段BC的大小关系是 .
其中正确的结论是(填写正确结论的序号).
13. 如图,张萌的手中有一张正方形纸片ABCD(AD∥BC),点E,F分别在AB个CD上,且EF∥AD,此时张萌判断出EF∥BC,则张萌判断出该结论的理由是 . 14. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
14. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)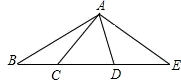 15. 将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2-∠1.能判断直线mn的有.(填序号)
15. 将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2-∠1.能判断直线mn的有.(填序号)
三、解答题(共9题,共70分)
-
16. 判断一个正整数能被3整除的方法是:把这个正整数各个数位上的数字相加,如果所得的和能够被3整除,则这个正整数就能被3整除.请证明对于任意两位正整数,这个判断方法都是正确的.17. 如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
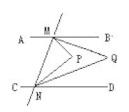 18. 如图①,ABCD,M为平面内一点,若BM⊥MC,则易证∠ABM与∠DCM互余.
18. 如图①,ABCD,M为平面内一点,若BM⊥MC,则易证∠ABM与∠DCM互余. (1)、如图②,ABCD.点M在射线EA上运动,猜想点M在点A和D之间时,∠BMC与∠ABM、∠DCM之间的数量关系,并证明.(2)、在(1)的条件下,当点M在射线EA的其它位置上时(不与点E,A,D重合)请直接写出∠BMC与∠ABM、∠DCM之间的数量关系.19. 阅读下列材料:
(1)、如图②,ABCD.点M在射线EA上运动,猜想点M在点A和D之间时,∠BMC与∠ABM、∠DCM之间的数量关系,并证明.(2)、在(1)的条件下,当点M在射线EA的其它位置上时(不与点E,A,D重合)请直接写出∠BMC与∠ABM、∠DCM之间的数量关系.19. 阅读下列材料:如图1, , , 分别是 , 上的点,点在 , 之间,连接 , . 用等式表示 , 与的数量关系.
小刚通过观察,实验,提出猜想: .
接着他对猜想的结论进行了证明,证明思路是:
过点作 , 由 , 可得 , 根据平行线的性质,可得 , , 从而证得 .

请你利用小刚得到的结论或解题思路,完成下列问题.
已知 , , 分别是 , 上的点,点在 , 之间,连接 , .
(1)、如图2,若 , , 则的度数为;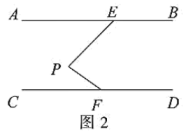 (2)、如图3,与的平分线交于点 , 用等式表示与的数量关系,并证明;
(2)、如图3,与的平分线交于点 , 用等式表示与的数量关系,并证明; (3)、如图4,与的平分线交于点 , 直接用等式表示与的数量关系.
(3)、如图4,与的平分线交于点 , 直接用等式表示与的数量关系. 20. 将下列推证过程补充完整.
20. 将下列推证过程补充完整. (1)、如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
(1)、如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.①BE== ;
②∠BAD== ;
③∠AFB==90°;
④S△ABC= .
(2)、如图2,AB∥CD,∠BAE=∠DCE=45°,∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
21. 我们常用以下的方法判断一个数字能否被三整除:例如一个三位数M,百位数字、十位数字、个位数字依次是a、b、c,如果a、b、c的和可以被三整除,那么就可以判断M可以被三整除.小明同学在学习过代数式的相关知识后,解释了这样判断的依据,请完成下面的说理过程:(1)、这个三位数M可以表示为;(2)、设k表示任意一个整数, 则a+b+c=(用含k的代数式表示);(3)、完成说理过程:因为M=a+b+c+() = ( ) +3()= 3(),而a、b、k都是整数,所以M可以被三整除.
22. (阅读与理解)小天同学看到如下的阅读材料:对于一个数A,以下给出了判断数A是否为19的倍数的一种方法:
每次划掉该数的最后一位数字,将划掉这个数字的两倍与剩下的数相加得到一个和,称为一次操作,依此类推,直到数变为20以内的数为止.若最后得到的数为19.则最初的数A就是19的倍数,否则,数A就不是19的倍数.
以为例,经过第一次操作得到55,经过第二次操作得到15, , . 所以436不是19的倍数.
当数A的位数更多时,这种方法依然适用.
 (1)、(操作与说理)
(1)、(操作与说理)当时,请你帮小天写出判断过程;
(2)、小天尝试说明方法的道理,他发现解决问题的关键是每次判断过程的第一次操作,后续的操作道理都与第一次相同,于是他列出了如下表格进行分析.请你补全小天列出的表格:说明:表示 , 其中 , a,b,c均为整数.
A
A的表达式
第一次操作得到的和,记为M(A)
436
436=10×43+6
M(436)=43+2×6
532
532=
M(532)=
863
863=10×86+3
M(863)=86+2×3
……
……
……
=
M()=
(3)、利用以上信息说明:当M()是19的倍数时,也是19的倍数.23. 若∠A与∠B的两边分别垂直,请判断这两个角的等量关系. (1)、如图1,∠A与∠B的关系是;如图2,∠A与∠B的关系是;(2)、若∠A与∠B的两边分别平行,试探索这两个角的等量关系,画图并证明你的结论.24. 探究:如图①, ,试说明 .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
(1)、如图1,∠A与∠B的关系是;如图2,∠A与∠B的关系是;(2)、若∠A与∠B的两边分别平行,试探索这两个角的等量关系,画图并证明你的结论.24. 探究:如图①, ,试说明 .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
解: ∵ .(已知)
∴ .()
同理可证, .
∵ ,
∴ .()
应用:如图②, ,点F在 之间, 与 交于点M, 与 交于点N.若 , ,则 的大小为度.
拓展:如图③,直线 在直线 之间,且 ,点 分别在直线 上,点Q是直线 上的一个动点,且不在直线 上,连结 .若 ,则 =度.