2023年浙教版数学八年级上册1.2 定义与命题 同步测试(培优版)
试卷更新日期:2023-08-12 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 下列选项中,能说明命题“两个锐角的和是锐角”是一个假命题的反例是( )A、 B、 C、 D、2. 下列句子中,属于命题的是( )A、直线和垂直吗? B、过线段的中点作的垂线 C、同旁内角不互补,两直线不平行 D、已知 , 求的值3. 下列语句中是命题的有( )个
⑴三角形的内角和等于 ;⑵如果 ,那么 ;⑶1月份有30天;⑷作一条线段等于已知线段;⑸一个锐角与一个钝角互补吗?
A、2 B、3 C、4 D、54. 下列说法错误的个数是( )①在同一平面内,两条直线的位置关系有:相交、垂直和平行;
②在同一平面内,过一点有且只有一条直线与这条直线平行;
③在同一平面内,过一点有且只有一条直线与这条直线垂直;
④垂直于同一条直线的两条直线互相平行;
⑤直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
⑥若两条平行线被第三条直线所截,则一组同旁内角的角平分线互相垂直.
A、2个 B、3个 C、4个 D、5个5. 判断命题“如果 , 那么”是假命题,只需举出一个反例,反例中的n可以为( )A、 B、 C、0 D、6. 下列命题中,真命题有( )①在同一平面内,两边分别平行的两角相等;②两条直线被第三条直线所截,内错角相等;③三角形的三条高线所在直线交于一点;④如果 , 那么;⑤过一点有且只有一条直线与已知直线平行
A、1个 B、2个 C、3个 D、4个7. 下列命题中真命题的个数是( )①经过直线外一点,有且只有一条直线与这条直线平行
②两直线平行,同旁内角相等
③4的平方根是
④的立方根是
A、1个 B、2个 C、3个 D、4个8. 下列命题是真命题的是( )A、过一点有且只有一条直线和已知直线平行 B、 , 则 C、与互为相反数,则与互为相反数 D、的平方根是29. 下列说法:①对顶角相等;②两条直线被第三条直线所截,同位角相等;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤直线外一点到这条直线的垂线,叫做点到直线的距离.其中真命题有( )A、1个 B、2个 C、3个 D、4个10. 下列命题:①立方根是它本身的数只有3个;②的立方根是与;③无立方根;④互为相反数的两个数的立方根也互为相反数;是真命题的是( )A、①② B、①③ C、①④ D、②④二、填空题(每空3分,共21分)
-
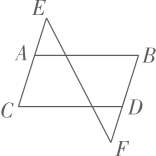
11. 将命题“等角的补角相等”改写成“如果……那么……”的形式,可写成 , 该命题是(填“真命题”或“假命题”).12. 把下列命题补充完整,使之成为真命题:“在同一平面内的直线a,b,c,若a⊥b,b∥c,则.”13. 能说明命题:“若两个角 , 互补,则这两个角必为一个锐角一个钝角”是假命题的反例是.14. 在说明命题“若|a|>3,则a>3”是假命题的反例中,a的值可以是 .15. 下列说法中:①两条直线被第三条直线所截,所得的内错角相等;②平面内,过一点有且只有一条直线与已知直线垂直;③三角形的三条高交于一点;④有公共顶点且相等的两个角是对顶角;⑤平行于同一条直线的两条直线平行;其中正确的个数是 .16. 如图,现有以下3个论断:①;②;③ . 如果以其中2个论断为条件,另一个论断为结论构造命题,能够构成个真命题.
三、解答题(共9题,共69分)
-
17. 判断下面命题的真假,若是假命题,请举出反例说明:
①一个三角形的3个内角中至少有1个钝角;
②若三条线段a , b , c满足a+b>c , 则这三条线段a , b , c能够组成三角形;
③个位数字是5的整数,能被5整除;
④对于所有的自然数n , 代数式n2-n+11的值都是质数;
18. 求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半. (1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
(1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.已知:在锐角中, , ▲ ;
求证: ▲ .
(2)、证明:19. 已知命题:“如图,点B、F、C、E在同一条直线上,则AB∥DE.”判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,在不添加其他辅助线的情况下,请添加一个适当的条件使它成为真命题,并加以证明. 20. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
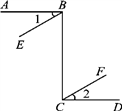
20. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性. 21. 如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
21. 如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
 22. 如图,Rt△ABC中,∠ACB=90°,D、E分别在边AB、AC上,给出下列信息:
22. 如图,Rt△ABC中,∠ACB=90°,D、E分别在边AB、AC上,给出下列信息:①BE平分∠ABC;②CD⊥AB;③∠CFE=∠CEF.
 (1)、请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个命题.在保证命题正确的情况下,你选择的条件是 , 结论是.(只要填写序号).(2)、请证明(1)中你组成的命题的正确性.23. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE∥AB , EF∥BC , 且DE交BC于点P . ∠ABC与∠DEF有怎样的数量关系?
(1)、请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个命题.在保证命题正确的情况下,你选择的条件是 , 结论是.(只要填写序号).(2)、请证明(1)中你组成的命题的正确性.23. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE∥AB , EF∥BC , 且DE交BC于点P . ∠ABC与∠DEF有怎样的数量关系? (1)、我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
(1)、我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.①图1中∠ABC与∠DEF数量关系为;图2中∠ABC与∠DEF数量关系为;
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): .
(2)、应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
24. 在数学课上,老师提出了这样一个问题:如图,点在的延长线上,请从①;②;③中,选取两个作为题设,第三个作为结论,组成一个命题,判断其真假,并证明.
小明的做法如下:选取①②作为题设,③作为结论.即“如果 , , 那么”是一个真命题.

证明:
(Ⅰ)
Ⅱ (Ⅱ)
(等量代换)
(1)、请帮助小明补全证明过程及推理依据;(2)、请作出与小明不同的选择,组成一个新的命题,判断其真假,并证明.25. 已知,和中, , . 试探究:(1)、如图1,写出与的关系,并说明理由;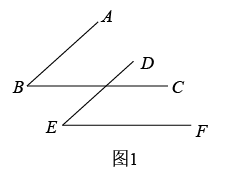 (2)、如图2,写出与的关系,并说明理由;
(2)、如图2,写出与的关系,并说明理由; (3)、根据上述探究,请归纳得到一个真命题.
(3)、根据上述探究,请归纳得到一个真命题.