广东省梅州市平远县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-12 类型:期末考试
一、单选题
-
1. 下列图形分别是平行四边形、矩形、菱形、正方形,其中不一定是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. “柳条初弄绿,已觉春风驻”.每到春天,人们在欣赏柳绿桃红的同时,也被飞舞的柳絮所烦恼,据了解柳絮纤维的直径约为0.00105cm,则0.00105用科学记数法可表示为( )A、 B、 C、 D、3. 用下列长度的三根木棒首尾相接,能做成三角形框架的是( )A、1,2,3 B、2,3,4 C、2,7,4 D、2,5,74. 下列计算正确的是( )A、 B、 C、 D、5. 下列计算中,能用平方差公式的是( )A、 B、 C、 D、6. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( )
2. “柳条初弄绿,已觉春风驻”.每到春天,人们在欣赏柳绿桃红的同时,也被飞舞的柳絮所烦恼,据了解柳絮纤维的直径约为0.00105cm,则0.00105用科学记数法可表示为( )A、 B、 C、 D、3. 用下列长度的三根木棒首尾相接,能做成三角形框架的是( )A、1,2,3 B、2,3,4 C、2,7,4 D、2,5,74. 下列计算正确的是( )A、 B、 C、 D、5. 下列计算中,能用平方差公式的是( )A、 B、 C、 D、6. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( ) A、 B、 C、 D、7. 如图,下列不能判定DF∥AC的条件是( )
A、 B、 C、 D、7. 如图,下列不能判定DF∥AC的条件是( ) A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°8. 如图,把长方形沿对折,若 , 则的度数等于( )
A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°8. 如图,把长方形沿对折,若 , 则的度数等于( ) A、25° B、50° C、100° D、115°9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )
A、25° B、50° C、100° D、115°9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )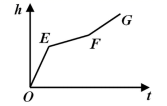 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( )
10. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( ) A、30° B、45° C、55° D、60°
A、30° B、45° C、55° D、60°二、填空题
-
11. 如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2= .
 12. 奥园路口红绿灯的时间设置为:红灯90秒,绿灯30秒,黄灯5秒.当人或车随意经过该路口时,遇到红灯的概率是 .13. 如图,已知与交于点, , 要使 , 添加一个你认为合适的条件为 .
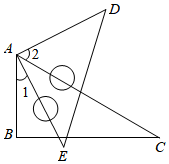
12. 奥园路口红绿灯的时间设置为:红灯90秒,绿灯30秒,黄灯5秒.当人或车随意经过该路口时,遇到红灯的概率是 .13. 如图,已知与交于点, , 要使 , 添加一个你认为合适的条件为 .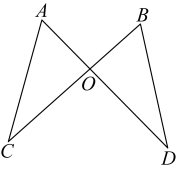 14. 多项式 是完全平方式,则m=.15. 张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:
14. 多项式 是完全平方式,则m=.15. 张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:重量/kg
1
2
3
…
售价/元
1.2+0.1
2.4+0.1
3.6+0.1
…
根据表中数据可知,若卖出柚子10kg,则售价为元.
16. 如图,是的中线, , 把沿对折,使点C落在点的位置,则图中的的形状是 17. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 .
17. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 .
三、解答题
-
18. 计算: .19. 先化简,再求值: , 其中 , .20. 在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数
100
150
200
500
800
1000
摸到白球的次数
59
96
116
290
480
601
摸到白球的频率
0.59
0.64
0.58
0.60
0.601
(1)、表中的a=;(2)、“摸到白球”的概率的估计值是(精确到0.1);(3)、试估算口袋中黑、白两种颜色的球各有多少个?21. 已知 在如图所示的平面直角坐标系中. (1)、直接写出三个顶点的坐标:A(),B(),C()(2)、将A、B、C三点的纵坐标保持不变,横坐标分别乘 ,得到点 、 、 ,在图中描出点 、 、 ,并画出 ;(3)、 边上的高为 .22. 小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:
(1)、直接写出三个顶点的坐标:A(),B(),C()(2)、将A、B、C三点的纵坐标保持不变,横坐标分别乘 ,得到点 、 、 ,在图中描出点 、 、 ,并画出 ;(3)、 边上的高为 .22. 小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题: (1)、在此变化过程中,自变量是 , 因变量是.(2)、小王在新华书店停留了多长时间?(3)、买到书后,小王从新华书店到商场的骑车速度是多少?23. 张老师用4张长为a、宽为b的小长方形(如图①)拼成了一个边长为的正方形(如图②)观察图形,回答下列问题:
(1)、在此变化过程中,自变量是 , 因变量是.(2)、小王在新华书店停留了多长时间?(3)、买到书后,小王从新华书店到商场的骑车速度是多少?23. 张老师用4张长为a、宽为b的小长方形(如图①)拼成了一个边长为的正方形(如图②)观察图形,回答下列问题: (1)、图②中,阴影部分的面积是;(2)、观察图①②,请你写出三个代数式:之间的关系 .(3)、应用:已知 , 求值:①;② .24. 如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)
(1)、图②中,阴影部分的面积是;(2)、观察图①②,请你写出三个代数式:之间的关系 .(3)、应用:已知 , 求值:①;② .24. 如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4) (1)、运动秒时,AE=DC;(2)、运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)、若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).25. 问题解决:
(1)、运动秒时,AE=DC;(2)、运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)、若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).25. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.