广东省河源市东源县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式从左到右的变形中，属于因式分解的是（）

A、（x＋3）（x-3）＝x²-9 B、2ab-2ac ＝2a（b-c） C、（m＋1）²＝m²＋2m＋1 D、n²＋2n＋1＝n（n＋2）＋1

查看试题解析
3. 若 $x < y$ 成立，则下列不等式成立的是（）

A、 $4 x < 3 y$ B、 $- x < - y$ C、 $\frac{x}{5} > \frac{y}{5}$ D、 $x + 6 < y + 6$

查看试题解析
4. 如图，在△ABC中，AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）

A、2 B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
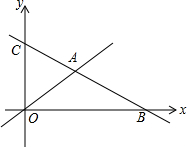
5. 如图，平行四边形ABCD中，AE平分∠DAB，∠B=100°，则∠DAE等于（）

A、100° B、80° C、60° D、40°

查看试题解析
6. 解分式方程 $\frac{x}{x - 1} - \frac{2}{x}$ ＝1时，去分母后变形为（）

A、x²-2＝1 B、x²-2（x-1）＝1 C、x²-2（x-1）＝x（x-1） D、x²-2x-1＝x（x-1）

查看试题解析
7. 下列每一组数据中的值分别为三角形的三边，不能构成直角三角形的（）

A、3、4、5 B、8、15、17 C、5、2、5 D、5、12、13

查看试题解析
8. 如图，一次函数 $y_{2} = - 2 x + n$ 与 $y_{1} = x + m$ 的图象交于点 $(1 ， 3)$ ，则关于 $x$ 的不等式 $x + m < - 2 x + n$ 的解集为（）

A、 $x > 1$ B、 $x < 1$ C、 $x > 3$ D、 $x < 3$

查看试题解析
9. 若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为 ( )

A、75°或15° B、30°或60° C、75° D、30°

查看试题解析
10. 如图，在平面直角坐标系中，将正方形 $O A B C$ 绕点 $O$ 逆时针旋转 $45 °$ 后得到正方形 $O A_{1} B_{1} C_{1}$ ，依此方式，绕点 $O$ 连续旋转2023次得到正方 $O A_{2023} B_{2023} C_{2023}$ ，如果点 $A$ 的坐标为 $(1 ， 0)$ ，那么 $B_{2023}$ 的坐标为（）

A、 $(1 ， 1)$ B、 $(\sqrt{2} ， 0)$ C、 $(- \sqrt{2} ， 0)$ D、 $(- 1 ， - 1)$

查看试题解析

二、填空题

11. 把多项式 $a^{2} - 9 b^{2}$ 分解因式结果是．

查看试题解析
12. 一个多边形的每个外角均为40°，则这个多边形的内角和为.

查看试题解析
13. 当 $x =$ 时，分式 $\frac{x + 1}{x^{}}$ 值为0.

查看试题解析
14. 若点 $A (6 - 2 x ， x - 5)$ 在平面直角坐标系的第二象限内，则x的取值范围是．

查看试题解析
15. 如图，点 $O$ 是 $△ A B C$ 内的一点， $O A = O B = O C$ ， $∠ B A C = 45 °$ ，则 $∠ B O C =$ ．

查看试题解析
16. 如图，将等腰直角 $△$ ABC沿BC方向平移得到 $△$ A₁B₁C₁ ．若BC＝3 $\sqrt{2}$ ， △ABC与 $△$ A₁B₁C₁重叠部分面积为2，则BB₁＝．

查看试题解析
17. 如图，▱ABCD中，∠DAB＝30°，AB＝6，BC＝2，P为边CD上的一动点，则2PB+ PD的最小值等于.

查看试题解析

三、解答题

18. 解不等式组： ${\begin{cases} 2 x - 1 < x + 5 \\ \frac{x + 1}{3} < x - 1 \end{cases}$

查看试题解析
19. 先化简，再求值： $(\frac{2 m + 1}{m} - 1) \div \frac{m^{2} - 1}{m}$ ，其中 $m = 2$ ．

查看试题解析
20. 已知：如图， $△ A B C$ 中， $D$ 是 $A B$ 中点， $D E ⊥ A C$ 垂足为 $E$ ， $D F ⊥ B C$ 垂足为 $F$ ，且 $E D = F D$ ，求证： $△ A B C$ 是等腰三角形

查看试题解析
21. 如图， $△ A B C$ 三个顶点坐标分别为 $A (1 ， 1)$ ， $B (4 ， 2)$ ， $C (3 ， 4)$ ．

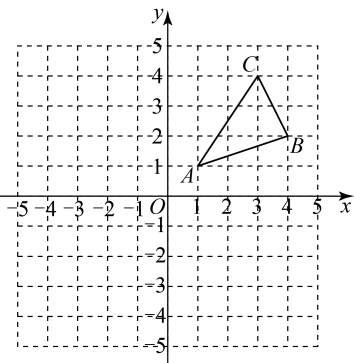(1)、请画出 $△ A B C$ 关于原点O成中心对称的图形 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、在x轴上找一点P ，使得 $P A + P B$ 的值最小，直接写出点P的坐标．

查看试题解析
22. 某地区以移动互联和大数据技术支持智慧课堂，实现学生的自主、个性和多元学习，全区学生逐步实现上课全部使用平板电脑.某商场用6万元购进甲种型号的平板，很快销售一空.该商场又用12.8万元购进了乙种型号的平板，所购数量是甲型平板购进数量的2倍，但单价贵了40元，甲型平板和乙型平板售价都是700元，但最后剩下的50件乙型平板按售价的八折销售，很快售完.

(1)、该商场购进甲型平板和乙型平板各多少元？

(2)、售完这两种平板，商场共盈利多少元？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， D为 $A B$ 边上一点，连接 $C D$ ， E为 $C D$ 中点，过点C作 $C F ∥ B D$ 交BE的延长线于F，连接 $D F$ 交 $A C$ 于点G，连接 $C F$ ．

(1)、求证：四边形 $D B C F$ 是平行四边形；

(2)、若 $∠ A = 30 °$ ， $B C = 4$ ， $C F = 6$ ，求四边形 $D B C F$ 的面积．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $L_{1}$ ： $y = - \frac{1}{2} x + 6$ 分别与x轴、y轴交于点B、C，且与直线 $L_{2}$ ： $y = \frac{1}{2} x$ 交于点A．

(1)、分别求出点A、B、C的坐标；

(2)、直接写出关于x的不等式 $- \frac{1}{2} x + 6 > \frac{1}{2} x$ 的解集；

(3)、若D是线段OA上的点，且 $△ C O D$ 的面积为12，求直线CD的函数表达式．

查看试题解析
25. 已知：如图， $△ A B C$ 、 $△ C D E$ 都是等边三角形， $A D$ 、 $B E$ 相交于点O，点M、N分别是线段 $A D$ 、 $B E$ 的中点．

(1)、求证： $A D = B E$ ；

(2)、求 $∠ D O E$ 的度数；

(3)、求证： $△ M N C$ 是等边三角形．

查看试题解析