广东省揭阳市榕城区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-12 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组线段的长为边,能组成三角形的是( )A、2、4、7 B、3、5、2 C、7、5、3 D、9、5、33. 下列说法正确的是( )A、两点之间,直线最短 B、不相交的两条直线叫做平行线 C、平面内,过一点有且只有一条直线与已知直线垂直 D、直线外一点到这条直线的垂线段叫做点到直线的距离4. 盒子里有10个球,它们只有颜色不同,其中红球有7个,黄球有2个,黑球有1个.幸幸从中任意摸一个球,下面说法正确的是( )A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小5. 等腰三角形的两条边长分别为15和7,则它的周长等于( )A、22 B、29 C、37 D、29或376. 如图,在中,直线为的垂直平分线,并交于点D,连接 . 若 , , 则的长为( )
2. 以下列各组线段的长为边,能组成三角形的是( )A、2、4、7 B、3、5、2 C、7、5、3 D、9、5、33. 下列说法正确的是( )A、两点之间,直线最短 B、不相交的两条直线叫做平行线 C、平面内,过一点有且只有一条直线与已知直线垂直 D、直线外一点到这条直线的垂线段叫做点到直线的距离4. 盒子里有10个球,它们只有颜色不同,其中红球有7个,黄球有2个,黑球有1个.幸幸从中任意摸一个球,下面说法正确的是( )A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小5. 等腰三角形的两条边长分别为15和7,则它的周长等于( )A、22 B、29 C、37 D、29或376. 如图,在中,直线为的垂直平分线,并交于点D,连接 . 若 , , 则的长为( ) A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,已知 , 增加下列条件:不能使的条件( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,已知 , 增加下列条件:不能使的条件( )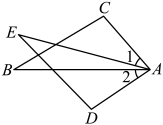 A、 B、 C、 D、9. 已知 , , 那么之间满足的等量关系是( )A、 B、 C、 D、10. 如图,点D、E分别是边、上一点, , , 连接交于点F,若的面积为12,则与的面积之差等于( )
A、 B、 C、 D、9. 已知 , , 那么之间满足的等量关系是( )A、 B、 C、 D、10. 如图,点D、E分别是边、上一点, , , 连接交于点F,若的面积为12,则与的面积之差等于( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 数据0.0000314用科学记数法可表示为 .12. 计算的结果是 .13. 某地高山上温度从山脚起每升高100米降低 , 已知山脚下温度是 , 则温度与上升高度x(米)之间关系式为 .14. 已知a,b,c是三角形的三边长,化简: .15. 如图,在 , , , , 是的中线,动点P从点A出发,以每秒的速度沿运动,最终到达点E.当点P运动s时,的面积等于 .

三、解答题
-
16. 如图,在中,D是边上的一点, .
 (1)、尺规作图:作平分 , 交于点E,连接(不写作法,保留作图痕迹);(2)、求证: .17. 先化简再求值: , 其中 .18. 如图,在长方形中, , , 点E为边上一动点,连接 , 随着点E的运动,的面积也发生变化.
(1)、尺规作图:作平分 , 交于点E,连接(不写作法,保留作图痕迹);(2)、求证: .17. 先化简再求值: , 其中 .18. 如图,在长方形中, , , 点E为边上一动点,连接 , 随着点E的运动,的面积也发生变化. (1)、写出的面积y与的长之间的关系式;(2)、当时,求y的值.19. 在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.(1)、分别求出摸出的球是红球和黄球的概率.(2)、为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?20. 如图,中, , , , 垂足为E.
(1)、写出的面积y与的长之间的关系式;(2)、当时,求y的值.19. 在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.(1)、分别求出摸出的球是红球和黄球的概率.(2)、为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?20. 如图,中, , , , 垂足为E. (1)、若 , 求的度数;(2)、若 , 求证: .21. 上小学时,我们已学过三角形三个内角的和为180°.定义:如果一个三角形的两个内角与满足 . 那么我们称这样的三角形为“准互余三角形”.
(1)、若 , 求的度数;(2)、若 , 求证: .21. 上小学时,我们已学过三角形三个内角的和为180°.定义:如果一个三角形的两个内角与满足 . 那么我们称这样的三角形为“准互余三角形”. (1)、若是“准互余三角形”, , , 则;(2)、若是直角三角形, .
(1)、若是“准互余三角形”, , , 则;(2)、若是直角三角形, .①如图,若AD是的平分线,请你判断是否为“准互余三角形”?并说明理由.
②点E是边BC上一点,是“准互余三角形”,若 , 则 ▲ .

