广东省梅州市蕉岭县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-12 类型:期末考试
一、单选题
-
1. 下列标志中,可以看作是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、
-
2. 将0.0000012用科学记数法表示应为( )A、 B、 C、 D、
-
3. 下列运算正确的是( ).A、 B、 C、 D、
-
4. 已知三角形的三边长分别为3,5, , 则不可能是( )A、3 B、5 C、7 D、8
-
5. 如图,下列条件中,不能判定的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6. “翻开人教版《数学》九年级上册课本恰好翻到第页”这个事件是( )A、随机事件 B、确定事件 C、不可能事件 D、必然事件
-
7. 如图,现有如下条件:; ;∠B=∠D; ∠B=∠DCE;⑤∠D+∠DCB=180°.其中能判断ABDC的有( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 已知b∥c,将一块含角的直角三角尺按如图的方式放置(等于),其中 , 两点分别落在直线 , 上,若 , 则为( )
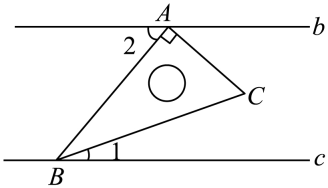 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
10. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( )
 A、30° B、45° C、55° D、60°
A、30° B、45° C、55° D、60°
二、填空题
-
11. 已知 , , 则 .
-
12. 如图,已知 ,则 之间的数量关系是
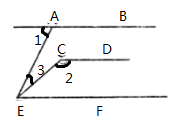
-
13. 奥园路口红绿灯的时间设置为:红灯90秒,绿灯30秒,黄灯5秒.当人或车随意经过该路口时,遇到红灯的概率是 .
-
14. 如图,已知与交于点, , 要使 , 添加一个你认为合适的条件为 .
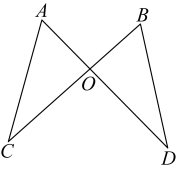
-
15. 变量x与y之间的关系是 , 当自变量x=2时,因变量y的值是.
-
16. 如图,点P为三边垂直平分线的交点,若 , , 则的度数为 .

-
17. 如图,四边形均为正方形,其中正方形面积为 . 图中阴影部分面积为 , 正方形面积为 .

三、解答题
-
18. 计算: .
-
19. 先化简,再求值:(2x-3)2+(x+4)(x-4)+5x(2-x),其中x=-.
-
20. 如图,EF//AD,∠1=∠2,∠BAC=82°,请将求∠AGD的过程填写完整.
解:因为EF//AD
所以∠2=∠ ▲ ( )
又因为∠1=∠2
所以∠1=∠3( )
所以AB// ▲ ( )
所以∠BAC+∠ ▲ =180°( )
因为∠BAC=82°
所以∠AGD= ▲ °

-
21. 已知: ABC.求作:射线BM,使它平分∠ABC,交AC于点M.(保留作图痕迹,不要求写作法,指明结果)

-
22. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式.(1)、若随机选一种方式进行支付,则恰巧是“现金”的概率是;(2)、在一次购物中,小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).
-
23. 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.
 (1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;当点D从B向C运动时,∠BDA逐渐变(填”大”或”小”);(2)、当DC=AB=2时,△ABD与△DCE是否全等?请说明理由:(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
(1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;当点D从B向C运动时,∠BDA逐渐变(填”大”或”小”);(2)、当DC=AB=2时,△ABD与△DCE是否全等?请说明理由:(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由. -
24. 如图1,在边长为的正方形中,点P从点A出发,沿A→B→C→D路线运动,到点D停止;点Q从点D出发,沿D→C→B→A路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒 , 点Q的速度为每秒 , a秒时点P、点Q同时改变速度,点P的速度为每秒 , 点Q的速度为每秒 , 图2是点P出发x秒后的面积与关系的图象.
 (1)、根据图象得;(2)、设点P已行的路程为 , 点Q还剩的路程为 , 试分别求出改变速度后,y1 , y2和出发后的运动时间x(秒)的关系式;(3)、若点P、点Q在运动路线上相距的路程为 , 求x的值.
(1)、根据图象得;(2)、设点P已行的路程为 , 点Q还剩的路程为 , 试分别求出改变速度后,y1 , y2和出发后的运动时间x(秒)的关系式;(3)、若点P、点Q在运动路线上相距的路程为 , 求x的值. -
25. 问题解决:
 (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
