广东省惠州市惠阳区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. $- 1$ ， $- \sqrt{2}$ ， 0， $\sqrt{3}$ 中最小的数是（）

A、 $- 1$ B、 $- \sqrt{2}$ C、0 D、 $\sqrt{3}$

查看试题解析
2. 下列调查方式中，适宜的是（　　）

A、合唱节前，某班为定制服装，对同学们的服装尺寸大小采用抽样调查 B、某大型食品厂为了解所生产的食品的合格率，采用全面调查 C、对乘坐某航班的乘客进行安检，采用全面调查 D、某市为了解该市中学生的睡眠情况，选取某中学初三年级的学生进行抽样调查

查看试题解析
3. 如图，如果 $A B / / C D$ ，那么（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 1 + ∠ 3 = 180 °$ D、 $∠ 4 + ∠ 2 = 180 °$

查看试题解析
4. 如图，用方向和距离描述图书馆相对于小青家的位置是（）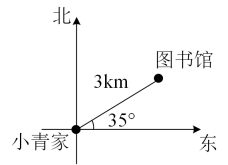

A、北偏东 $35 °$ ， 3km B、北偏东 $55 °$ ， 3km C、东偏北 $35 °$ D、东偏北 $55 °$ ， 3km

查看试题解析
5. 下列命题是真命题的是（）

A、同位角相等 B、内错角相等 C、相等的角是对顶角 D、同旁内角互补，两直线平行

查看试题解析
6. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{- 4} = 2$ C、 $\sqrt[3]{- 64} = - 4$ D、 $\sqrt{2 \frac{7}{9}} = \frac{5}{9}$

查看试题解析
7. 如果a＞b，那么下列结论一定正确的是（）

A、a-3＜b-3 B、3-a＞3-b C、 $- \frac{a}{3} ＜ - \frac{b}{3}$ D、-3a＞-3b

查看试题解析
8. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程 $a x + b y = 3$ 的解，则代数式 $a + 2 b - 5$ 的值为（）

A、0 B、 $- 1$ C、 $- 2$ D、 $- 3$

查看试题解析
9. 一个正数m的平方根是2a+3与1-a，则关于x的不等式 $a x + \sqrt{m} < 0$ 的解集为（）

A、 $x > \frac{5}{4}$ B、 $x < \frac{5}{4}$ C、 $x > \frac{4}{5}$ D、 $x < \frac{4}{5}$

查看试题解析
10. 明代《算法统宗》有一首饮酒数学诗：“醇酒一瓶醉三客，薄酒三瓶醉一人，共同饮了一十九，三十三客醉颜生，试问高明能算士，几多醇酒几多薄？”这首诗是说：“好酒一瓶，可以醉倒3位客人；薄酒三瓶，可以醉倒1位客人，如今33位客人醉倒了，他们总共饮19瓶酒．试问：其中好酒、薄酒分别是多少瓶？”设有好酒x瓶，薄酒y瓶．根据题意，可列方程组为（）

A、 ${\begin{array}{l} x + y = 19 \\ 3 x + \frac{1}{3} y = 33 \end{array}$ B、 ${\begin{array}{l} x + y = 19 \\ x + 3 y = 33 \end{array}$ C、 ${\begin{array}{l} x + y = 19 \\ \frac{1}{3} x + 3 y = 33 \end{array}$ D、 ${\begin{array}{l} x + y = 19 \\ 3 x + y = 33 \end{array}$

查看试题解析

二、填空题

11. 计算： $- 5 + 2 =$ ．

查看试题解析
12. 一个样本中的数据最大值是140，最小值是40，若取组距为12，则可以分成组．

查看试题解析
13. 在平面直角坐标系中，已知点 $M (m - 1 ， 2 m + 4)$ 在 $x$ 轴上，则点 $M$ 的坐标为．

查看试题解析
14. 已知 $∠ A$ 的两边与 $∠ B$ 的两边分别平行，且 $∠ A$ 比 $∠ B$ 的 $2$ 倍少 $18 °$ ，那么 $∠ A =$

查看试题解析
15. 已知方程组 ${\begin{array}{l} 2 x + 4 y = k \\ x - y = k + 3 \end{array}$ 的解 $x$ ， $y$ 之和为 $2$ ，则 $k =$ ．

查看试题解析
16. 对于实数a，b，c，d，定义 $| \begin{array}{l} a & c \\ b & d \end{array} | = a d - b c$ ，已知 $- 2 < | \begin{array}{l} 2 & 4 \\ 3 & x \end{array} | \leq 4$ ，则x的取值范围是.

查看试题解析

三、解答题

17. 解方程组 ${\begin{array}{l} x - y = 4 \\ 4 x + 2 y = - 1 \end{array}$ .

查看试题解析
18. 计算： $| - 3 | + \sqrt{16} + \frac{1}{2} \times \sqrt[3]{- 8}$

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 (x - 1) + 1 > - 3 ， \\ x - 1 \leq \frac{1 + x}{3} ， \end{array}$ 并把它的解集在数轴上表示出来．

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (- 4 ， 3)$ ， $B (- 2 ， 4)$ ， $C (- 1 ， 1)$ ，把 $△ A B C$ 向右平移 $5$ 个单位长度，再向下平移 $3$ 个单位长度得到 $△ A^{'} B^{'} C^{'}$ ，点 $A$ ， $B$ ， $C$ 的对应点分别为 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ．

(1)、写出 $A^{'}$ ， $C^{'}$ 的坐标；

(2)、在图中画出平移后的 $△ A^{'} B^{'} C^{'}$ ；

(3)、求 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析
21. 某市为了解初中生每周锻炼身体的时长 $t$ （单位：小时）的情况，在全市随机抽取部分初中生进行调查，按五个组别：A组（ $3 \leq t < 4$ ）；B组（ $4 \leq t < 5$ ）；C组（ $5 \leq t < 6$ ）；D组（ $6 \leq t < 7$ ）；E组（ $7 \leq t < 8$ ）进行整理，绘制成如下两幅不完整的统计图，根据图中提供的信息，解决下列问题：

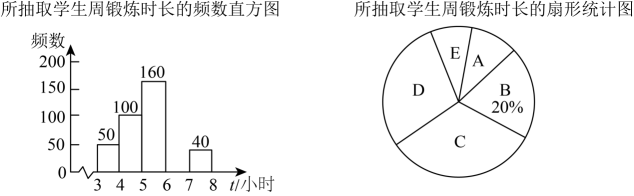(1)、求出这次抽样调查的学生总人数；

(2)、补全频数分布直方图；

(3)、C组所在扇形的圆心角的度数为度；

(4)、根据样本估计全市12000名初中生中，每周锻炼身体的时长不少于5小时的有多少名．

查看试题解析
22. 如图所示，已知 $∠ CFE + ∠ BDC = 180^{°} ， ∠ DEF = ∠ B$ ，试判断 $∠ A E D$ 与 $∠ A C B$ 的大小关系，并说明理由.

查看试题解析
23. 某工厂承接了一批纸箱加工任务，用如图 $1$ 所示的长方形和正方形纸板 $($ 长方形的宽与正方形的边长相等 $)$ 加工成如图所示的竖式与横式两种无盖的长方形纸箱（加工时接缝材料不计）

(1)、若该厂购进正方形纸板 $1000$ 张，长方形纸板 $2000$ 张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；

(2)、该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板 $80$ 张，长方形纸板 $a$ 张，全部加工成上述两种纸盒，且 $150 < a < 171$ ，试求在这一天加工两种纸盒时， $a$ 的所有可能值．

查看试题解析
24. 对 $x$ ， $y$ 定义一种新运算 $T$ ，规定： $T (x ， y) = \frac{a x + b y}{x + y}$ （其中 $a$ ， $b$ 均为非零常数），这里等式右边是通常的四则运算，例如： $T (0 ， 1) = \frac{a \times 0 + b \times 1}{0 + 1} = b$ ，已知 $T (1 ， 1) = 2.5$ ， $T (4 ， - 2) = 4$ ．

(1)、求 $a$ ， $b$ 的值；

(2)、若关于 $m$ 的不等式组 ${\begin{array}{l} \begin{array}{l} T (4 m ， 5 - 4 m) \leq 3 \end{array} \\ T (2 m ， 3 - 2 m) ＞ P \end{array}$ 恰好有2个整数解，求实数 $P$ 的取值范围．

查看试题解析
25. 如图1，在平面直角坐标系中， $A (a ， 0)$ ， $C (b ， 2)$ ，且满足 $\sqrt{a + 2} + {(b - 2)}^{2} = 0$ ，过C作 $C B ⊥ x$ 轴于B．

(1)、求△ABC的面积；

(2)、若过B作 $B D ∥ A C$ 交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数；

(3)、在y轴上存在点P使得△ABC和△ACP的面积相等，请直接写出P点坐标．

查看试题解析