广东省潮州市潮安区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、 $\sqrt{4}$ B、 $\frac{2}{3}$ C、﹣ $\sqrt{5}$ D、0

查看试题解析
2. 在平面直角坐标系中，点 $(4 ， - 3)$ 所在象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，与∠1是同旁内角的是（）

A、∠2 B、∠3 C、∠4 D、∠5

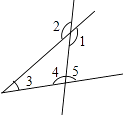查看试题解析
4. 如图，直线 $a ∥ b$ ，将三角尺的直角顶点放在直线 $b$ 上，若 $∠ 1 = 35 °$ ，则 $∠ 2$ 等于（）

A、 $45 °$ B、 $55 °$ C、 $35 °$ D、 $65 °$

查看试题解析
5. 如果a＞b，下列不等式中不正确的是（）

A、a-4＞b-4 B、-a+2＞-b+2 C、2a+1＞2b+1 D、-3a＜-3b

查看试题解析
6. 已知 $| x ＋ y ＋ 1 | ＋$ $\sqrt{2 x - y}$ $= 0$ ，则 $x - y$ 的值为（　）

A、 $- \frac{1}{3}$ B、 $- 1$ C、 $\frac{1}{3}$ D、1

查看试题解析
7. 下列调查中，最适合采用普查方式的是（）

A、对重庆市辖区内长江流域水质情况的调查 B、对乘坐飞机的旅客是否携带违禁物品的调查 C、对一个社区每天丢弃塑料袋数量的调查 D、对重庆电视台“天天630”栏目收视率的调查

查看试题解析
8. 已知 $| a | = 4$ ， $b^{2} = 9$ ，且 $\frac{a}{b} > 0$ ，求 $a - b$ 的值（）

A、1或 $- 1$ B、5或 $- 5$ C、5 D、1

查看试题解析
9. 关于x的不等式组 ${\begin{array}{l} x > a \\ x > 1 \end{array}$ 的解集为 $x > 1$ ，则 $a$ 的取值范围是（）

A、 $a > 1$ B、 $a < 1$ C、 $a \geq 1$ D、 $a \leq 1$

查看试题解析
10. 已知方程组 ${\begin{array}{l} x + y = 1 - a ， \\ x - y = 3 a + 5 \end{array}$ 的解x为正数，y为非负数，给出下列结论：① $- 1 < a \leq 1$ ；②当 $a = - \frac{5}{3}$ 时， $x = y$ ；③当 $a = - 2$ 时，方程组的解也是方程 $x + y = 5 + a$ 的解；④若 $0 < x \leq 1$ ，则 $2 \leq y < 4$ .其中正确的是（）

A、①② B、②③ C、①④ D、②③④

查看试题解析

二、填空题

11. 9的算术平方根是．

查看试题解析
12. 在平面直角坐标系中，点A的坐标为（-4，3）．若线段AB∥y轴，且AB的长为6，则点B的坐标为．

查看试题解析
13. 已知关于x、y的方程组 ${\begin{array}{l} x + 3 y = 3 - a \\ 2 x + y = 1 + 3 a \end{array}$ 的解满足 $x + y > 3 a + 4$ ，求a的取值范围.

查看试题解析
14. 如图，点E在AC的延长线上，给出的四个条件：

(1)、 $∠ 3 = ∠ 4$ ；（2） $∠ 1 = ∠ 2$ ；（3） $∠ A = ∠ D C E$ ；（4） $∠ D + ∠ A B D = 180 °$ 能判断 $A B ∥ C D$ 的有个.

查看试题解析
15. 如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为 $(1 ， 0)$ 、 $(2 ， 0)$ 、 $(2 ， 1)$ 、 $(1 ， 1)$ 、 $(1 ， 2)$ 、 $(2 ， 2)$ …根据这个规律，第2023个点的坐标．

查看试题解析

三、解答题

16. 计算：

(1)、计算： $| \sqrt{3} - 2 | - \sqrt[3]{- 27} - \sqrt{(- 3)^{2}} + \sqrt{16}$

(2)、解方程组： ${\begin{array}{l} 6 x + 5 y = 31 ， ① \\ 3 x + 2 y = 13 ； ② \end{array}$

查看试题解析
17. 解不等式组 ${\begin{cases} 5 x + 1 > 3 (x - 1) \\ \frac{x - 1}{2} \geq 2 x - 4 \end{cases}$ ，并求出它的整数解．

查看试题解析
18. 小辰想用一块面积为 $100 c m^{2}$ 的正方形纸片，沿着边的方向裁出一块面积为 $90 c m^{2}$ 的长方形纸片，使它的长宽之比为 $5 ： 3$ . 小辰能否用这张正方形纸片裁出符合要求的纸片？若能请写出具体裁法；若不能，请说明理由.

查看试题解析
19. 我市某中学全校师生参加了由学校开展的党史知识竞赛活动，随机抽查了部分师生的成绩，经过整理并制作了还不完整的频数分布表和频数分布直方图
分数x（分）
频数
百分比
$60 \leq x < 70$
30
$10 %$
$70 \leq x < 80$
90
n
$80 \leq x < 90$
m
$40 %$
$90 \leq x \leq 100$
60
$20 %$
请根据图表提供的信息，解答下列问题：

(1)、本次调查的样本容量为；

(2)、在频数分布表中m= ▲ ；n= ▲ ；并补全频数分布直方图；

(3)、如果竞赛成绩在80分以上（含80分）为“优秀”，那么该校师生2000人中，成绩为“优秀”的大约是多少人？

查看试题解析
20. 如图， $A C / / E F$ ， $∠ 1 + ∠ 3 = 180 °$ ．

(1)、求证： $A F / / C D$ ；

(2)、若 $A C ⊥ E B$ 于点 $C$ ， $∠ 2 = 40 °$ ，求 $∠ B C D$ 的度数．

查看试题解析
21. 已知：如图所示的网格中，每个小正方形的边长均为1个长度单位， $△ A B C$ 的顶点A的坐标为 $(0 ， 5)$ .

(1)、根据A点的坐标在网格中建立平面直角坐标系，并写出点B、C两点的坐标，

(2)、将 $△ A B C$ 向下平移4个单位，再向右平移1个单位得 $△ A^{'} B^{'} C^{'}$ ，画出 $△ A^{'} B^{'} C^{'}$ ，写出 $A^{'} ， B^{'} ， C^{'}$ 的坐标

(3)、求 $S_{△ A B C}$ .

查看试题解析
22. 去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．

(1)、求饮用水和蔬菜各有多少件？

(2)、现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；

(3)、在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？

查看试题解析
23. 如图，点A的坐标为 $(1 ， 0)$ ，点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为 $(- 3 ， 2)$ ．

(1)、点E的坐标为；点B的坐标为；

(2)、在四边形ABCD中，点P从点B出发，沿“ $B C \to C D$ ”移动．
①当点P在CD上时﹐设 $∠ C B P = x ， ∠ P A D = y ， ∠ B P A = z$ ，试用含x，y的式子表示z，写出解答过程．

②当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐求点P的坐标．

查看试题解析

分数x（分）	频数	百分比
$60 \leq x < 70$	30	$10 %$
$70 \leq x < 80$	90	n
$80 \leq x < 90$	m	$40 %$
$90 \leq x \leq 100$	60	$20 %$