（单元测试B卷）第三章整式及其加减—2023-2024学年北师大版七年级数学上册

试卷更新日期：2023-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列合并同类项中，正确的是（　　）

A、 $2 x + 3 y = 5 x y$ B、 $3 x^{2} + 2 x^{3} = 5 x^{5}$ C、 $- 2 x^{2} + 2 x^{2} = x^{2}$ D、 $x^{2} - 3 x^{2} = - 2 x^{2}$

查看试题解析
2. 已知 $a - 2 b = - 1$ ，则代数式 $1 - 2 a + 4 b$ 的值是（）

A、-3 B、-1 C、2 D、3

查看试题解析
3. 某种商品进价为a元，在销售旺季，提价30%销售，旺季过后，商品以7折价格开展促销活动，这时一件商品的售价为（）

A、a B、0.7a C、1.03a D、0.91a

查看试题解析
4. 下列说法正确的是（）

A、 $\frac{1}{x} + 1$ 是多项式 B、 $\frac{3 x + y}{3}$ 是单项式 C、 $- m n^{5}$ 是五次单项式 D、 $- x^{2} y - 2 x^{3} y$ 是四次多项式

查看试题解析
5. 按如图所示的运算程序，能使输出 $y$ 值为 $5$ 的是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 2$ ， $n = 0$ C、 $m = 2$ ， $n = 2$ D、 $m = 3$ ， $n = 2$

查看试题解析
6. 1883年，康托尔用以下的方法构造的这个分形，称做康托尔集.如图，取一条长度为1的线段，将它三等分，去掉中间一段，留剩下两段，这称为第一阶段；然后将剩下的两段再三等分，各去掉中间一段，剩下更短的四段，这称为第二阶段…将这样的操作无限地重复下去，余下的无穷点就称做康托尔集.那么经过第四个阶段后，留下的线段的长度之和为（）

A、 $\frac{4}{27}$ B、 $\frac{16}{81}$ C、 $\frac{8}{243}$ D、 $\frac{16}{243}$

查看试题解析
7. 找出以下图形变化的规律，则第 2022 个图形中黑色正方形的数量是（）

A、3030 B、3031 C、3032 D、3033

查看试题解析
8. 【阅读理解】计算：25×11＝275，13×11＝143，48×11＝528，74×11＝814，观察算式，我们发现两位乘11的速算方法：头尾一拉，中间相加，满十进一.
【拓展应用】已知一个两位数，十位上的数字是a，个位上的数字是b，这个两位数乘11，计算结果的十位上的数字可表示为（　　）

A、a或a＋1 B、a＋b或ab C、a＋b−10 D、a＋b或a＋b−10

查看试题解析
9. 已知数a，b，c在数轴上的位置如图所示，化简|a+b|-|a-b|+|c-a|的结果为（）

A、-3a+c B、a-2b-c C、-a-2b+c D、-a+2b+c

查看试题解析
10. 如图，用三个同图①的长方形和两个同图②的长方形用两种方式去覆盖一个大的长方形ABCD，两种方式未覆盖的部分(阴影部分)的周长相等，那么图①中长方形的面积S₁与图②中长方形的面积S₂的比是（）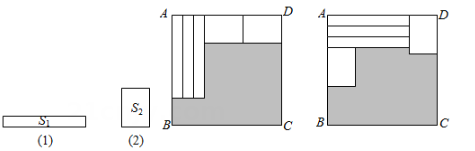

A、2：3 B、1：2 C、3：4 D、1：1

查看试题解析

二、填空题（每空3分，共15分）

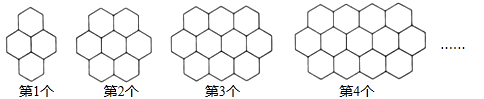
11. 若 $x^{2} - 3 x + 6$ 的值为5，则 $3 x^{2} - 9 x - 6$ 的值为.

查看试题解析
12. 历史上数学家欧拉最先把关于x的多项式用记号 $f (x)$ 来表示，把x等于某数a时的多项式的值用 $f (a)$ 来表示.例如，对于多项式 $f (x) = m x^{3} + n x + 5$ ，当 $x = 2$ 时，多项式的值为 $f (2) = 8 m + 2 n + 5$ .若对于多项式 $f (x) = t x^{5} + m x^{3} + n x + 7$ ，有 $f (3) = 6$ ，则 $f (- 3)$ 的值为.

查看试题解析
13. 如图，观察下列的“蜂窝图”，则第n个图案中的正六边形的个数是（用含n的代数式表示）.

查看试题解析
14. 如图是一组有规律的图案，它们是由边长相等的等边三角形组合而成，照此规律摆下去，摆成第50个图案需要个等边三角形．

查看试题解析
15. 已知 $x ， y ， z$ 都是有理数， $x + y + z = 0$ ， $x y z \neq 0$ ，则 $\frac{| x |}{y + z} + \frac{| y |}{x + z} + \frac{| z |}{x + y}$ 的值是．

查看试题解析

三、解答题（共8题，共75分）

16. 观察 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ =（1－ $\frac{1}{2}$ ）+（ $\frac{1}{2}$ － $\frac{1}{3}$ ）=1－ $\frac{1}{3}$ = $\frac{2}{3}$

(1)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +……+ $\frac{1}{2013 \times 2014}$

(2)、计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots \dots + \frac{1}{99 \times 101}$

查看试题解析
17. 先化简，再求值： $9 (\frac{1}{9} x^{2} - \frac{2}{3} x + 1) - 4 (\frac{1}{4} x^{2} + x + 2) - 10$ ，其中 $x = 3$ .

查看试题解析
18. 小明化简 $(4 a^{2} - 2 a - 6) - 2 (2 a^{2} - 2 a - 5)$ 的过程如下，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程：
解： $(4 a^{2} - 2 a - 6) - 2 (2 a^{2} - 2 a - 5)$
$= 4 a^{2} - 2 a - 6 - 4 a^{2} + 4 a + 5 ①$
$= (4 - 4) a^{2} + (- 2 + 4) a + (- 6 + 5) ②$
$= 2 a - 1 ③$
他化简过程中出错的是第 ▲ 步 $($ 填序号 $)$ ；
正确的解答是：

查看试题解析
19. 某会所在一个长方形的空地上修建两个扇形游泳池（阴影部分），如图所示，两个游泳池之间的空地上铺上五彩石.（单位：米）

(1)、请用含 $a$ ， $b$ 的代数式表示铺五彩石的空地的面积；（结果保留 $π$ ）

(2)、如果 $a = 25$ ， $b = 10$ ，每平方米的五彩石的价格为100元，求购买五彩石的总费用.（ $π$ 取3.14）

查看试题解析
20. 甲、乙两家超市以相同的价格出售同样的商品，但为了吸引顾客，各自推出不同的优惠方案.在甲超市累计购买商品超过400元后，超出的部分按原价 $70 %$ 收取：在乙超市购买商品只按原价的 $80 %$ 收取.设某顾客预计累计购物x元.

(1)、当 $x > 400$ 时，分别用代数式表示顾客在两家超市购物所付的费用；

(2)、当 $x = 1000$ 时，该顾客应选择哪一家超市购物比较合算?说明理由.

查看试题解析
21. 某农户承包果树若干亩，今年投资 $12800$ 元，收获水果总产量为 $18000$ 千克.此水果在市场上每千克售x元，在果园直接销售每千克售y元（ $y < x$ ），该农户将水果拉到市场出售平均每天出售 $1000$ 千克.

(1)、若这批水果全部在市场上销售，则需要天.

(2)、两种方式出售水果的收入
①水果在市场上销售为元（用含x的代数式表示）；
②水果在果园直接销售为元（用含y的代数式表示）.

(3)、若售完全部水果.当 $y = 4$ 元时，请你计算水果在果园直接销售的利润.（利润 $=$ 收入 $-$ 支出）

查看试题解析
22. 有7张如图1规格相同的小长方形纸片，长为a，宽为b（ $a > b$ ），按如图2、3的方式不重叠无缝隙地放在矩形 $A B C D$ 内，未被覆盖的部分（两个矩形）用阴影表示．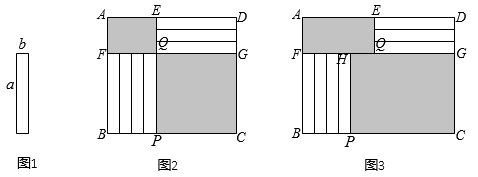

(1)、如图2，点E、Q、P在同一直线上，点F、Q、G在同一直线上，那么矩形ABCD的面积为．（用含a、b的代数式表示）

(2)、如图3，点F、H、Q、G在同一直线上，设右下角与左上角的阴影部分的面积的差为S， $P C = x$ ．
①用a、b、x的代数式直接表示AE

②当BC的长度变化时，按照同样的放置方式，如果S的值始终保持不变，那么a、b必须满足什么条件？

查看试题解析
23. 【教材呈现】如图是人教版七年级上册数学教材76页的部分内容．

把 $(a + b)$ 和 $(x + y)$ 各看作一个整体，对下列各式进行化简：

⑴ $4 (a + b) + 2 (a + b) - (a + b)$ ；……

(1)、【问题解决】对（1）中的式子进行化简，写出化简过程：

(2)、【简单应用】
①已知 $a^{2} + a = 1$ ，则 $2 a^{2} + 2 a + 2020 =$ ▲ ；

②已知 $a + b = - 3$ ，求 $5 (a + b) + 7 a + 7 b + 11$ 的值；

(3)、【拓展提高】
已知 $a^{2} - 2 a b = - 5$ ， $a b + 2 b^{2} = - 3$ ，求代数式 $3 a^{2} - \frac{9}{2} a b + 3 b^{2}$ 的值．

查看试题解析

（单元测试B卷）第三章 整式及其加减—2023-2024学年北师大版七年级数学上册

一、选择题（每题3分，共30分）

二、填空题（每空3分，共15分）

三、解答题（共8题，共75分）

（单元测试B卷）第三章整式及其加减—2023-2024学年北师大版七年级数学上册