2023年七年级上册数学人教版单元分层测试第二章整式的加减 B卷

试卷更新日期：2023-08-10 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列说法中，正确的是（）

A、 $- \frac{1}{2} x^{2} y$ 的系数是 $\frac{1}{2}$ B、 $x^{2} - 1$ 的常数项是1 C、 $4 x^{2} y$ 次数是2次 D、 $2 x^{2} - x + 2$ 是二次多项式

查看试题解析
2. 已知-4a与一个多项式的积是 $16 a^{3} + 12 a^{2} + 4 a$ ，则这个多项式是（）

A、 $- 4 a^{2} + 3 a$ B、 $4 a^{2} - 3 a$ C、 $4 a^{2} - 3 a + 1$ D、 $- 4 a^{2} - 3 a - 1$

查看试题解析
3. 现用同品质的A，B两种钢板制作某产品，有如下两种用料方案：方案1用5块A型钢板，9块B型钢板：方案2用4块A型钢板，10块B型钢板．已知每块A型钢板的面积比B型钢板大．设每块A型钢板和B型钢板的面积分别为x和y．从省料角度考虑，应选（）

A、方案1 B、方案2 C、方案1与方案2都一样 D、无法确定

查看试题解析
4. 有若干个形状大小完全相同的小长方形，现将其中 $3$ 个如图 $1$ 摆放，构造一个正方形；其中 $5$ 个如图 $2$ 摆放，构造一个新的长方形 $($ 各小长方形之间不重叠且不留空隙 $) .$ 若图 $1$ 和图 $2$ 中阴影部分的面积分别为 $39$ 和 $106$ ，则每个小长方形的面积为（）

A、 $12$ B、 $14$ C、 $16$ D、 $18$

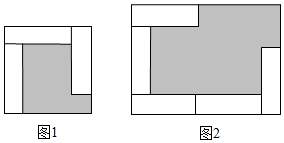查看试题解析

5. 在日历上，某些数满足一定的规律．如图是某年8月份的日历，任意选择其中所示的含4个数字的方框部分，设右上角的数字为a，则下列叙述中正确的是（）．

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

A、左上角的数字为

a + 1

B、左下角的数字为

a + 7

C、右下角的数字为

a + 8

D、方框中4个位置的数相加，结果是4的倍数

查看试题解析

6. 在矩形 $A B C D$ 内，将一张边长为a的正方形纸片和两张边长为b的正方形纸片（ $a > b$ ），按图1，图2两种方式放置（两个图中均有重叠部分），矩形中未被这三张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $S_{1}$ ，图2中阴影部分的面积为 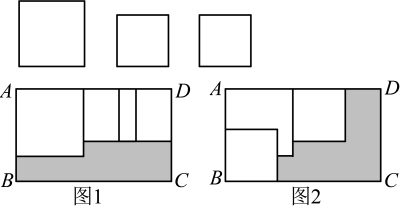$S_{2}$ ，当 $A D - A B = 2$ 时， $S_{1} - S_{2}$ 的值是（　　）

A、 $2 a$ B、 $2 b$ C、 $- 2 b + b^{2}$ D、 $2 a - 2 b$

查看试题解析
7. 记 $n = (1 + 3) (1 + 3^{2}) (1 + 3^{4}) \dots (1 + 3^{256})$ ，则 $2 n + 1$ （）

A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方

查看试题解析
8. 如图，在长方形 $A B C D$ 中放入一个边长为8的大正方形 $A L M N$ 和两个边长为6的小正方形（正方形 $D E F G$ 和正方形 $H I J K$ ）.3个阴影部分的面积满足 $2 S_{3} + S_{1} - S_{2} = 2$ ，则长方形 $A B C D$ 的面积为（）

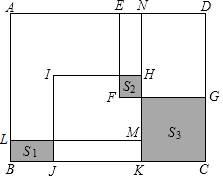A、90 B、96 C、98 D、100

查看试题解析

二、填空题

9. 化简： $3 a^{2} - a (2 a - 1) =$ .

查看试题解析
10. 若 $(x^{2} + m x - 8) (x^{2} - 3 x + n)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，则 $n$ 的值为．

查看试题解析
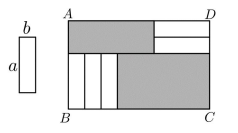
11. 若一个四位正整数（各个数位均不为0），百位数字比千位数字小3，个位数字比十位数字小2，则称该数为“和平数”，例如：4131，9642都是“和平数”，将一个四位正整数 $P$ 的百位和十位交换位置后得到四位数 $Q ， G (P) = \frac{P - Q}{90}$ ，若 $P$ 为“和平数”，且 $P$ 能被9整除，则满足条件的所有 $P$ 值中， $G (P)$ 的最大值是．

查看试题解析
12. 如图，5张长为a，宽为b(a>b)的小长方形纸片，不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示。设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，S始终保持不变，则a，b满足的关系是．

查看试题解析

三、计算题

13. 计算下列各题：

(1)、 ${(2 x^{2} y)}^{3} \cdot (- 7 x y^{2}) \div 14 x^{4} y^{3}$ ；

(2)、 $[(2 x + y) (x - y) + y^{2}] \div 2 x$ ．

查看试题解析

四、解答题

14. 化简求值： $3 x^{2} y - [2 xy - 2 (xy - \frac{3}{2} x^{2} y) + xy]$ ，其中x＝3， $y = - \frac{1}{3}$ ．

查看试题解析
15. 如果关于 $x$ 的多项式 $(3 x^{2} + 2 m x - x + 1) + (2 x^{2} - m x + 5) - (5 x^{2} - 4 m x - 6 x)$ 的值与 $x$ 无关，你能确定 $m$ 的值吗？并求 $m^{2} + (4 m - 5) + m$ 的值 $.$

查看试题解析
16. 某县学校分为初中部和小学部，做广播操时，两部分别站两个不同的操场上进行，站队时，做到了整齐划一，初中部排成的是一个规范的长方形方阵，每排 $(3 a - b)$ 人，站有 $(3 a + 2 b)$ 排；小学部站的方阵更特别，排数和每排人数都是 $2 (a + b)$ .试求：该县直学校初中部比小学部多多少名学生；

查看试题解析

五、综合题

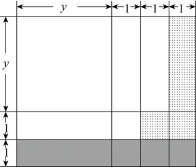
17. 已知口，⋆、△分别代表1∼9中的三个自然数．

(1)、如果用⋆△表示一个两位数，将它的个位和十位上的数字交换后得到一个新的两位数Δ⋆，若⋆Δ与Δ⋆的和恰好为某自然数的平方，则该自然数是；

(2)、如果在一个两位数⋆Δ前揷入一个数口后得到一个三位数口⋆△，设⋆△代表的两位数为x，口代表的数为y，则三位数口⋆Δ用含x，y的式子可表示为；

(3)、设a表示一个两位数，b表示一个三位数，把a放在b的左边组成一个五位数m，再把b放在a的左边、组成一个新五位数n．试探索：m-n能否被9整除？并说明你的理由．

查看试题解析
18. 给出如下定义：我们把有序实数对 $(a ， b ， c)$ 叫做关于x的二次多项式 $a x^{2} + b x + c$ 的特征系数对，把关于x的二次多项式 $a x^{2} + b x + c$ 叫做有序实数对 $(a ， b ， c)$ 的特征多项式.

(1)、关于x的二次多项式 $3 x^{2} + 2 x - 1$ 的特征系数对为；

(2)、求有序实数对 $(1 ， 4 ， 4)$ 的特征多项式与有序实数对 $(1 ， - 4 ， 4)$ 的特征多项式的乘积；

(3)、若有序实数对 $(p ， q ， - 1)$ 的特征多项式与有序实数对 $(m ， n ， - 2)$ 的特征多项式的乘积的结果为 $2 x^{4} + x^{3} - 10 x^{2} - x + 2$ ；直接写出 $(4 p - 2 q - 1) (2 m - n - 1)$ 的值为.

查看试题解析
19. 提出问题：怎么运用矩形面积表示（y+2）（y+3）与2y+5的大小关系（其中y>0）？
几何建模：
（1）画长y+3，宽y+2的矩形，按图方式分割
（2）变形：2y+5=（y+2）+（y+3）
（3）分析：图中大矩形的面积可以表示为（y+2）（y+3）；阴影部分面积可以表示为（y+3）×1，画点部分的面积可表示为y+2，由图形的部分与整体的关系可知：

（y+2）（y+3）＞（y+2）+（y+3），即（y+2）（y+3）＞2y+5

归纳提炼：

当a>2，b>2时，表示ab与a+b的大小关系．根据题意，设a=2+m，b=2+n（m>0，n>0），要求参照上述研究方法，画出示意图，并写出几何建模步骤（用铅笔画图，并标注相关线段的长）

查看试题解析

20. 阅读下面材料，完成相应的任务：

阿贝尔公式

数学界三大奖项之一的阿贝尔奖，是为了纪念挪威著名数学家阿贝尔所设．阿贝尔是近代数学发展的先驱，他年轻时利用阶梯图形，发现了重要的恒等式——阿贝尔公式．

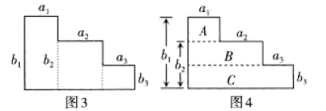
如右图，用两种方法将一个二级阶梯图形分别分割成两个长方形．按图1的方法，该阶梯图形的面积为 $a_{1} b_{1} + a_{2} b_{2}$ ；按图2的方法，长方形①的面积为 $a_{1} (b_{1} - b_{2})$ ，长方形②的面积为 $(a_{1} + a_{2}) b_{2}$ ，根据图1、图2面积相等，可得到二级阶梯图形对应的阿贝尔公式： $a_{1} b_{1} + a_{2} b_{2} = a_{1} (b_{1} - b_{2}) + (a_{1} + a_{2}) b_{2}$ ．

任务：

(1)、推理验证：材料中的阿贝尔公式可用代数运算验证，请补全如下说理过程：

因为右边＝．

左边＝a₁b₁＋a₂b₂ ，左边＝右边，

所以，a₁b₁＋a₂b₂＝a₁（b₁－b₂）＋（a₁＋a₂）b₂ ．

(2)、类比探究：如下图，用两种方法将一个三级阶梯图形分别分割成三个长方形．

①图4中长方形B的长为a₁＋a₂ ，宽为 ▲ ；

②由图3、图4面积相等，可得三级阶梯图形对应的阿贝尔公式为：a₁b₁＋a₂b₂＋a₃b₃＝a_l（b_l－b₂）＋ ▲ ＋ ▲ ．

请补全该公式，并进行验证．