2023年七年级上册数学人教版单元分层测试第二章整式的加减 A卷

试卷更新日期：2023-08-10 类型：单元试卷

进入出卷网下载

一、选择题

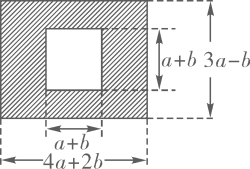
1. 下列说法正确的是（）

A、 $- \frac{2}{3} x y^{2}$ 的次数是2 B、 $\frac{1}{a}$ 是单项式 C、 $2 a^{2} - 3 a b c - 1$ 是三次三项式 D、 $- 2 π a b^{2}$ 的系数是 $- 2$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \times a^{4} = a^{12}$ C、 $(a^{3})^{4} = a^{12}$ D、 $a^{8} \div a^{4} = a^{2}$

查看试题解析
3. 若单项式 $a^{m - 1} b^{2}$ 与 $\frac{1}{2} a^{2} b^{n}$ 的和仍是单项式，则 $n^{m}$ 的值是（）

A、6 B、4 C、9 D、8

查看试题解析
4. 已知 $2 a^{x} b^{3}$ 与 $- a^{2} b^{1 - y}$ 是同类项，则 $x y$ 的值为（）

A、4 B、 $- 4$ C、 $- 3$ D、6

查看试题解析
5. 下列整式中，是二次单项式的是（）

A、 $x^{2} + 1$ B、 $x y$ C、 $x^{2} y$ D、 $- 3 x$

查看试题解析
6. 下列运算正确的是（）

A、 $2 x + y = 2 x y$ B、 ${(- 3 a^{2} b)}^{2} = 6 a^{4} b^{2}$ C、 ${(x + y)}^{2} = x^{2} + y^{2}$ D、 $(a^{2} - a b) \div a = a - b$

查看试题解析
7. 已知 $▲ \cdot (- 2 x y) = 4 x^{2} y - 6 x y^{2}$ ，则 $▲ =$ （）

A、 $- 2 x + 3 y$ B、 $2 x + 3 y$ C、 $- 2 x - 3 y$ D、 $2 x - 3 y$

查看试题解析
8. 若 $S = 3 x^{2} - 2 x y + y^{2}$ ， $T = x^{2} + 2 x y - y^{2}$ ，则 $S$ 与 $T$ 的大小关系为（）

A、 $S > T$ B、 $S < T$ C、 $S \geq T$ D、 $S \leq T$

查看试题解析
9. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个因式分解的等式．观察如图的长方形，可以得到的因式分解是（）

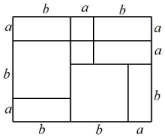A、 $(a + b) (2 a + b) = 2 a^{2} + 3 a b + b^{2}$ B、 $2 a^{2} + 3 a b + b^{2} = (a + b) (2 a + b)$ C、 $2 a^{2} + 5 a b + 2 b^{2} = (a + 2 b) (2 a + b)$ D、 $2 a^{2} + 4 a b + 2 b^{2} = 2 (a + b)^{2}$

查看试题解析
10. 在长方形ABCD内，将一张边长为a的正方形纸片和两张边长为b的正方形纸片（ $a > b$ ），按图1，图2两种方式放置（两个图中均有重叠部分），矩形中未被这三张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $s_{1}$ ，图2中阴影部分的面积为 $s_{2}$ ，当 $A D - A B = 2$ 时，若知道下列条件，能求 $s_{1} - s_{2}$ 值的是（）

A、边长为a的正方形的面积 B、边长为b的正方形的面积 C、边长为a的正方形的面积与两个边长为b的正方形的面积之和 D、边长a与b之差

查看试题解析

二、填空题

11. 若单项式 $- 3 a^{m - 1} b$ 与 $2 a^{2} b$ 是同类项，则 $m$ 的值是．

查看试题解析
12. 把多项式 $6 x - 7 x^{2} + 9$ 按字母 $x$ 的降幂排列为．

查看试题解析
13. 多项式 $17 x^{4} + 9 x^{2} - 1$ 的常数项是．

查看试题解析
14. 已知正方形的边长为 $a$ ，如果它的边长增加6，那么它的面积增加．

查看试题解析
15. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下： $\times 2 x = 4 x^{2} - 6 x y + 2 x$ ，则所指的多项式为．

查看试题解析
16. 如图长方形 $A B C D$ 由图1、2、3、4、5拼成，设图1、2、3是边长分别为a，b，c $(a < b < c)$ 的正方形，图4是长方形，图5是正方形．对于判断：① $a + b > c$ ；②图4的周长为 $3 b + c$ ；③ $a + c = 2 b$ ；④长方形 $A B C D$ 的周长为 $2 (a + b + c)$ ，其中正确的是（填编号）．

查看试题解析

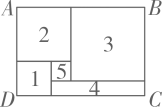
三、计算题

17. 计算： $- 3 x^{2} \cdot 2 y + {(2 x y^{2})}^{3} \div (- 2 x y^{5})$

查看试题解析
18. 计算： $3 (2 a - 1) (2 a + 1) - 2 (a + 2) (a - 3)$ ．

查看试题解析

四、解答题

19. 有这样一道题，计算： $(x - y) [{(x + y)}^{2} - x y] - (x - y) [{(x - y)}^{2} + x y] - 2 x y (x - y) + 3 x^{2}$ 的值，其中 $x = 3 ， y = 4$ ；某同学把“ $y = 4$ ”错抄成“ $y = 3$ ”但他的计算结果是正确的，请回答这是怎么回事？试说明理由 $.$

查看试题解析
20. 眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为(4a+2b)米，宽为(3a-b)米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为（a+b）米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当a=20，b=10时的绿化面积．

查看试题解析
21. 发现：当两个不同的正整数同为偶数或奇数时，这两个数之和与这两个数之差的平方差一定能被4整除，且这两个数的积可以表示为两个正整数的平方差．
验证：如， ${(3 + 1)}^{2} - {(3 - 1)}^{2} = 12$ 能被4整除，请把3与1的积写成两个正整数的平方差；

探究：设“发现”中两个正整数分别为m，n，请论证“发现”中的结论正确．

查看试题解析

2023年七年级上册数学人教版单元分层测试 第二章 整式的加减 A卷

一、选择题

二、填空题

三、计算题

四、解答题

2023年七年级上册数学人教版单元分层测试第二章整式的加减 A卷