(单元测试B卷)第一章 丰富的图形世界—2023-2024学年北师大版七年级数学上册
试卷更新日期:2023-08-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
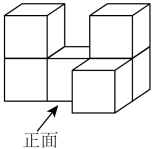
1. 如图是由6个小正方体拼成的几何体,该几何体从上面看到的形状图是( )
 A、
A、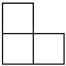 B、
B、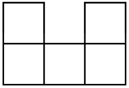 C、
C、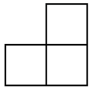 D、
D、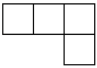 2. 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成(第6题图)体,则下列序号中不应剪去的是( )
2. 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成(第6题图)体,则下列序号中不应剪去的是( )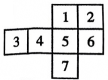 A、6 B、3 C、2 D、13. 如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则a-b+c的值为( )
A、6 B、3 C、2 D、13. 如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则a-b+c的值为( )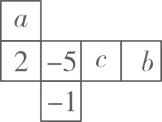 A、6 B、4 C、2 D、-44. 在下面的图形中,不是正方体的展开图的是( )A、
A、6 B、4 C、2 D、-44. 在下面的图形中,不是正方体的展开图的是( )A、 B、
B、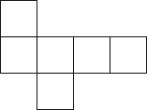 C、
C、 D、
D、 5. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、
5. 下列几何体都是由大小相同的小正方体组成,其中左视图与主视图相同的几何体是( )A、 B、
B、 C、
C、 D、
D、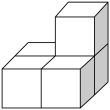 6. 如图,这是一个正方体的表面展开图,六个面上各有一字,连起来是“全面落实双减”,把它折成正方体后,与“落”相对的字是( )
6. 如图,这是一个正方体的表面展开图,六个面上各有一字,连起来是“全面落实双减”,把它折成正方体后,与“落”相对的字是( )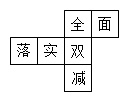 A、面 B、实 C、双 D、减7. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )
A、面 B、实 C、双 D、减7. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )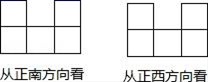 A、12个 B、13个 C、14个 D、18个8. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .
A、12个 B、13个 C、14个 D、18个8. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .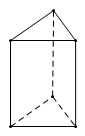 A、28 B、31 C、34 D、369. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
A、28 B、31 C、34 D、369. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )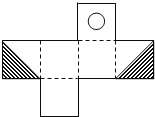 A、
A、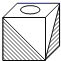 B、
B、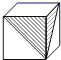 C、
C、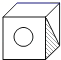 D、
D、 10. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )
10. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )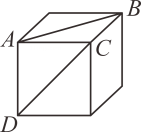 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共15分)
-
11. 如图,用一个平面去截一个三棱柱,截面的形状可能是.
①三角形②四边形③五边形④六边形
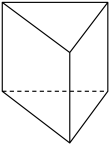 12. 某正方体的每一个面上都有一个汉字,它的一种表面展开图如图所示,那么在原正方体中,与“喜”字所在面相对面上的汉字是 .
12. 某正方体的每一个面上都有一个汉字,它的一种表面展开图如图所示,那么在原正方体中,与“喜”字所在面相对面上的汉字是 .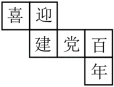 13. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .
13. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .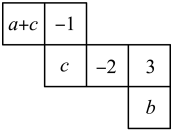 14. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.15. 一个由许多规格相同的小正方体堆积而成的几何体,其主视图、左视图如图所示一模一样,若要摆成这样的图形,至少需用 m 块小正方体,至多需用n 块小正方体,则 mn= .
14. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.15. 一个由许多规格相同的小正方体堆积而成的几何体,其主视图、左视图如图所示一模一样,若要摆成这样的图形,至少需用 m 块小正方体,至多需用n 块小正方体,则 mn= .
三、解答题(共8题,共75分)
-
16. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,求a﹣b的值.
 17. 如图所示是一个用小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请你画出它的主视图与左视图.
17. 如图所示是一个用小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请你画出它的主视图与左视图. 18. 如图是长方体的展开图,若图中的正方形边长为6cm,长方形的长为8cm,宽为6cm,请求出由展开图折叠而成的长方体的表面积和体积.
18. 如图是长方体的展开图,若图中的正方形边长为6cm,长方形的长为8cm,宽为6cm,请求出由展开图折叠而成的长方体的表面积和体积.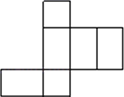 19. 如图是由一些棱长为1的相同的小正方体组合成的简单几何体.
19. 如图是由一些棱长为1的相同的小正方体组合成的简单几何体. (1)、请在相应方格纸中分别画出该几何体的视图;(2)、这个几何体的表面积是.20. 如图,在一个正方形网格中有五个小正方形,每个面上分别标有一个数值,在网格中添上一个正方形,使之能折叠成一个正方体,且使相对面上的两个数字之和相等.
(1)、请在相应方格纸中分别画出该几何体的视图;(2)、这个几何体的表面积是.20. 如图,在一个正方形网格中有五个小正方形,每个面上分别标有一个数值,在网格中添上一个正方形,使之能折叠成一个正方体,且使相对面上的两个数字之和相等.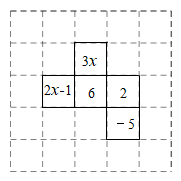 (1)、在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)(2)、求添上的正方形面上的数值.21. 如图所示是长方体的平面展开图.
(1)、在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)(2)、求添上的正方形面上的数值.21. 如图所示是长方体的平面展开图.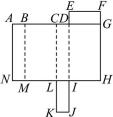 (1)、将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?(2)、若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?22. 【问题情境】
(1)、将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?(2)、若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?22. 【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.

【操作探究】
(1)、图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)、小圣所在的综合实践小组把折叠成6个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.
23. 如图1是边长为 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计). (1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:
(1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:1
2
3
4
5
6
7
8
324
588
576
500
252
128
填空:① , ;
②由表格中的数据观察可知当 的值逐渐增大时, 的值.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)