广东省汕尾市2022-2023学年高一下学期期末数学试题
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 若复数是纯虚数,则实数( )A、1 B、0或1 C、1或2 D、1或32. 已知 , , , 则( )A、 B、 C、 D、或3. 将函数的图象向左平移个周期后所得图象对应的函数为( )A、 B、 C、 D、4. 已知直线 , , 和平面 , 则下列命题正确的是( )A、若 , , 则 B、若 , , , , 则 C、若 , , , , 则 D、若 , , 则5. 已知 , , 则( )A、 B、 C、 D、6. 在正三棱柱中,为棱的中点, , 则直线与直线所成角的余弦值为( )A、0 B、 C、 D、7. 在中,内角 , , 所对的边分别为 , , , , , 则( )A、 B、 C、 D、8. 如图,在边长为2的正方形中, , 分别是 , 的中点,将 , , 分别沿 , , 折起,使得三点重合于点 , 若三棱锥的所有顶点均在球的球面上,则球的体积为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知复数 , , 则下列说法正确的有( )A、 B、 C、 D、在复平面内 , 对应的点关于虚轴对称10. 已知函数 , , 且的最小正周期为 , 则下列说法正确的有( )A、 B、当时,的最小值为1 C、在区间上单调递增 D、若为偶函数,则正实数的最小值为11. 下列说法正确的有( )A、若 , 满足 , , 则的最大值为3 B、向量在向量上的投影向量为 C、若 , , 且 , 则 D、若圆中,弦的长为4,则12. 在棱长为2的正方体中, , 分别为棱 , 的中点,则( )A、直线与直线是异面直线 B、直线与直线共面 C、直线与平面所成角的正弦值为 D、点到平面的距离为
三、填空题
-
13. 化简.14. 已知圆锥的表面积为 ,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是 .15. 在平行四边形中, , , , 则.16. 如图是古希腊数学家希波克拉底研究的几何图形,此图由三个半圆构成,直径分别是直角三角形的斜边 , 直角边 , , 点在以为直径的半圆上,延长 , 交于点.若 , , , 则的面积是.

四、解答题
-
17. 已知点 , , .(1)、若 , 是实数,且 , 求的值;(2)、求与的夹角的余弦值.18. 已知函数.(1)、求的最小正周期;(2)、在中,若 , 求的最大值.19. 如图,在正方体中, , 分别为棱 , 的中点,是线段上的动点.证明:
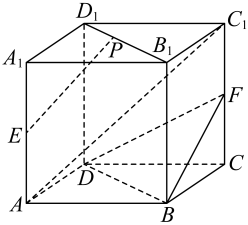 (1)、平面;(2)、平面.
(1)、平面;(2)、平面.