河北省“五个一”名校联盟2022-2023学年高二下学期期末联考数学试题
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 设集合 , , 则下列结论正确的是( )A、 B、 C、 D、2. 已知 , , , 则与夹角的余弦值为( )A、-1 B、 C、0 D、13. 已知双曲线与双曲线 , 则两双曲线的( )A、实轴长相等 B、虚轴长相等 C、离心率相等 D、焦距相等4. 已知 , 且 , 则下列各式一定成立的是( )A、 B、 C、 D、5. 一条长椅上有6个座位,3个人坐.要求3个空位中恰有2个空位相邻,则坐法的种数为( )A、36 B、48 C、72 D、966. 某学校有男生600人,女生400人.为调查该校全体学生每天的运动时间,采用分层抽样的方法获取容量为的样本.经过计算,样本中男生每天运动时间的平均值为80分钟,方差为10;女生每天运动时间的平均值为60分钟,方差为20.结合数据,估计全校学生每天运动时间的方差为( )A、96 B、110 C、112 D、1287. 过直线上一点向圆O:作两条切线,设两切线所成的最大角为 , 则( )A、 B、 C、 D、8. 设是定义在上的奇函数,且满足 , . 数列满足 , , 则( )A、0 B、-1 C、2 D、-2
二、多选题
-
9. 若 , , 则下列说法正确的是( )A、若事件相互独立,则事件也互斥 B、若事件相互独立,则事件不互斥 C、若事件互斥,则事件也相互独立 D、若事件互斥,则事件不相互独立10. 函数由关系式确定,则下列说法正确的是( )A、函数的零点为1 B、函数的定义域和值域均为 C、函数的图象是轴对称图形 D、若 , 则在定义域内满足恒成立11. 某通信工具在发送、接收信号时都会使用数字0或是1作为代码,且每次只发送一个数字.由于随机因素的干扰,发出的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收成0或1的概率分别为0.94和0.06;发送信号1时,接收成1或0的概率分别为0.96和0.04.假设发送信号0或1的概率是等可能的,则( )A、已知两次发送的信号均为1,则接收到的信号均为1的概率为 B、在单次发送信号中,接收到0的概率为0.49 C、在单次发送信号中,能正确接收的概率为0.95 D、在发送三次信号后,恰有两次接收到0的概率为12. 已知为等腰直角三角形,为斜边且长度是 . 为等边三角形,若二面角为直二面角,则下列说法正确的是( )A、 B、三棱锥的体积为 C、三棱锥外接球的表面积为 D、半径为的球可以被整体放入以三棱锥为模型做的容器中
三、填空题
-
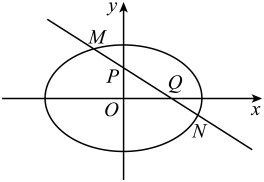
13. 方程在复数集中的解为 .14. .15. 已知函数的图像关于点对称,且在区间上单调,则 .16. 如图所示,斜率为的直线交椭圆于M、N两点,交轴、轴分别于Q、P两点,且 , 则椭圆的离心率为 .
四、解答题
-
17. 已知数列的前n项和为 , 数列满足 , .(1)、证明:数列是等差数列;(2)、是否存在常数p、q,使得对一切正整数n都有成立?若存在,求出p、q的值;若不存在,说明理由.18. 记的内角A、B、C的对边分别为a、b、c,且 .(1)、求角的大小;(2)、设边上的高 , 求面积的最小值.19. 如图,圆锥的高为3,是底面圆的直径,PC,PD为圆锥的母线,四边形是底面圆的内接等腰梯形,且 , 点在母线上,且 .
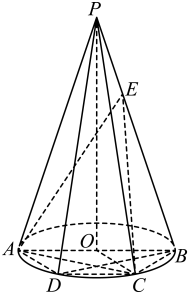 (1)、证明:平面平面;(2)、求平面与平面的夹角的余弦值.20. 已知函数 .(1)、讨论函数的单调性;(2)、若既有极大值又有极小值,且极大值和极小值的和为 . 解不等式 .21. 已知为抛物线上一点, , 为的中点,设的轨迹为曲线 .(1)、求曲线的方程;(2)、过点作直线交曲线E于点M、N,点为直线l:上一动点.问是否存在点使为正三角形?若存在,求出点坐标;若不存在,请说明理由.22. 航天事业是国家综合国力的重要标志,带动着一批新兴产业和新兴学科的发展.某市为了激发学生对航天科技的兴趣,点燃学生的航天梦,现组织该市全体学生参加航天创新知识竞赛,并随机抽取1000名学生作为样本,研究其竞赛成绩.经统计分析该市高中生竞赛成绩近似地服从正态分布 , 其中近似为样本平均数 , 近似为样本方差 , 并已求得和 .
(1)、证明:平面平面;(2)、求平面与平面的夹角的余弦值.20. 已知函数 .(1)、讨论函数的单调性;(2)、若既有极大值又有极小值,且极大值和极小值的和为 . 解不等式 .21. 已知为抛物线上一点, , 为的中点,设的轨迹为曲线 .(1)、求曲线的方程;(2)、过点作直线交曲线E于点M、N,点为直线l:上一动点.问是否存在点使为正三角形?若存在,求出点坐标;若不存在,请说明理由.22. 航天事业是国家综合国力的重要标志,带动着一批新兴产业和新兴学科的发展.某市为了激发学生对航天科技的兴趣,点燃学生的航天梦,现组织该市全体学生参加航天创新知识竞赛,并随机抽取1000名学生作为样本,研究其竞赛成绩.经统计分析该市高中生竞赛成绩近似地服从正态分布 , 其中近似为样本平均数 , 近似为样本方差 , 并已求得和 .(附: , , , , , 若 , 则 , )
(1)、若该市有4万名高中生,试估计这些高中生中竞赛成绩位于区间的人数;(2)、若规定成绩在85.2以上的学生等级为优秀,现从全市高中生中任意抽取一个进行访谈,如果取到学生等级不是优秀,则继续抽取下一个,直至取到等级为优秀的学生为止,但抽取的总次数不超过 . 如果抽取次数的期望值不超过6,求的最大值.