四川省遂宁市2022-2023学年高二下学期期末数学理科试题
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 设是虚数单位,若复数 , 则的共轭复数为( )A、 B、 C、 D、2. 命题“ , ”的否定为( )A、 , B、 , C、 , D、 ,3. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 设函数在定义域内可导,其图象如图所示,则导函数的图象可能是( )
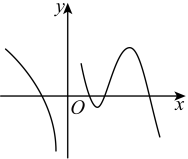 A、
A、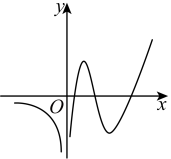 B、
B、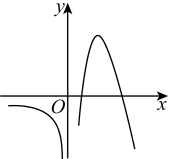 C、
C、 D、
D、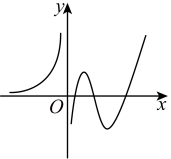 5. 已知抛物线的焦点为 , 抛物线上有一动点 , , 则的最小值为( )A、10 B、16 C、11 D、266. “燃脂单车”运动是一种在音乐的烘托下,运动者根据训练者的指引有节奏的踩踏单车,进而达到燃脂目的的运动,由于其操作简单,燃脂性强,受到广大健身爱好者的喜爱.已知某一单车爱好者的骑行速度v(单位:km/h)随时间t(单位:h)变换的函数关系为 , , 则该单车爱好者骑行速度的最大值为( )A、 B、 C、 D、7. 短道速滑队6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔,记“甲得第一名”为p,“乙得第二名”为q,“丙得第三名”为r,若是真命题,是假命题,是真命题,则选拔赛的结果为( )A、甲得第一名,乙得第二名,丙得第三名 B、甲得第二名,乙得第一名,丙得第三名 C、甲得第一名,乙得第三名,丙得第二名 D、甲得第一名,乙没得第二名,丙得第三名8. 要排出某班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学排在上午(前4节),体育课排在下午(后2节),不同排法种数是( )A、720 B、192 C、180 D、1449. 已知圆 , 若双曲线的一条渐近线与圆C相切,则( )A、 B、 C、 D、810. 若函数的最小值是 , 则实数m的取值范围是( )A、 B、 C、 D、11. 已知 , 则( )A、 B、 C、 D、12. 已知椭圆C:的左、右焦点分别为 , , 点M是椭圆C上任意一点,且的取值范围为 . 当点M不在x轴上时,设的内切圆半径为m,外接圆半径为n,则mn的最大值为( ).A、 B、 C、 D、1
5. 已知抛物线的焦点为 , 抛物线上有一动点 , , 则的最小值为( )A、10 B、16 C、11 D、266. “燃脂单车”运动是一种在音乐的烘托下,运动者根据训练者的指引有节奏的踩踏单车,进而达到燃脂目的的运动,由于其操作简单,燃脂性强,受到广大健身爱好者的喜爱.已知某一单车爱好者的骑行速度v(单位:km/h)随时间t(单位:h)变换的函数关系为 , , 则该单车爱好者骑行速度的最大值为( )A、 B、 C、 D、7. 短道速滑队6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔,记“甲得第一名”为p,“乙得第二名”为q,“丙得第三名”为r,若是真命题,是假命题,是真命题,则选拔赛的结果为( )A、甲得第一名,乙得第二名,丙得第三名 B、甲得第二名,乙得第一名,丙得第三名 C、甲得第一名,乙得第三名,丙得第二名 D、甲得第一名,乙没得第二名,丙得第三名8. 要排出某班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学排在上午(前4节),体育课排在下午(后2节),不同排法种数是( )A、720 B、192 C、180 D、1449. 已知圆 , 若双曲线的一条渐近线与圆C相切,则( )A、 B、 C、 D、810. 若函数的最小值是 , 则实数m的取值范围是( )A、 B、 C、 D、11. 已知 , 则( )A、 B、 C、 D、12. 已知椭圆C:的左、右焦点分别为 , , 点M是椭圆C上任意一点,且的取值范围为 . 当点M不在x轴上时,设的内切圆半径为m,外接圆半径为n,则mn的最大值为( ).A、 B、 C、 D、1二、填空题
-
13. 的展开式中的系数为 .14. 已知方程表示椭圆,则实数k的取值范围是 .15. 设双曲线的左、右焦点分别为 , , 为双曲线右支上一点,且 , 则的大小为 .16. 已知函数在处的切线斜率为 , , 若在上恒成立,则能取到的最大正整数为
三、解答题
-
17. 分别求适合下列条件的方程:(1)、长轴长为10,焦距为4的椭圆标准方程;(2)、经过点的抛物线的标准方程.18. 已知函数的图象过点 , 且在点P处的切线恰好与直线垂直.(1)、求函数的解析式;(2)、若函数在区间上单调递增,求实数m的取值范围.19. 党的二十大报告提出:“必须坚持科技是第一生产力、人才是第一资源、创新是第一动力,深入实施科教兴国战略、人才强国战略、创新驱动发展战略,开辟发展新领域新赛道,不断塑造发展新动能新优势.”某数字化公司为加快推进企业数字化进程,决定对其核心系统DAP,采取逐年增加研发人员的办法以提升企业整体研发和创新能力.现对2018~2022年的研发人数作了相关统计(年份代码1~5分别对应2018~2022年)如下折线图:

参考数据:当认为两个变量间的相关性较强
参考公式相关系数 ,
回归方程中的斜率和截距的最小二乘法估计公式分别为 , .
(1)、根据折线统计图中数据,计算该公司研发人数与年份代码的相关系数 , 并由此判断其相关性的强弱;(2)、试求出关于的线性回归方程,并预测2023年该公司的研发人数(结果取整数).20. 为提高学生的数学应用能力和创造力,学校打算开设“数学建模”选修课,为了解学生对“数学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认为感兴趣的人数占70%.附: , 其中.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)、根据所给数据,完成下面的列联表,并根据列联表判断是否有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关?感兴趣
不感兴趣
合计
男生
12
女生
5
合计
30
(2)、若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记选出高三女生的人数为X,求X的分布列与数学期望.